Question

Find the distance between \[P\left( {{x}_{1}},{{y}_{1}} \right)\] and \[Q\left( {{x}_{2}},{{y}_{2}} \right)\] when
(i) PQ is parallel to the y – axis and
(ii) PQ is parallel to the x – axis.

Answer 1

Hint: Consider part (i) of the given question and draw a diagram in which PQ is shown parallel to y – axis. Find the relation between \[{{x}_{1}}\] and \[{{x}_{2}}\] and then apply the distance formula given as \[PQ=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\] to get the answer. Similarly, consider part (ii) of the question and draw a diagram in which PQ is shown parallel to x – axis. Find the relation between \[{{y}_{1}}\] and \[{{y}_{2}}\] in this case and apply the same distance formula to get the answer.

Complete step by step answer:
Here we have been provided with two points P and Q having the coordinates \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] respectively. Two cases are provided to us and we have to determine the distance between P and Q in both the cases. So, let us check these cases one by one.
(i) When PQ is parallel to y-axis
In this case, one of the possible diagrams can be shown as

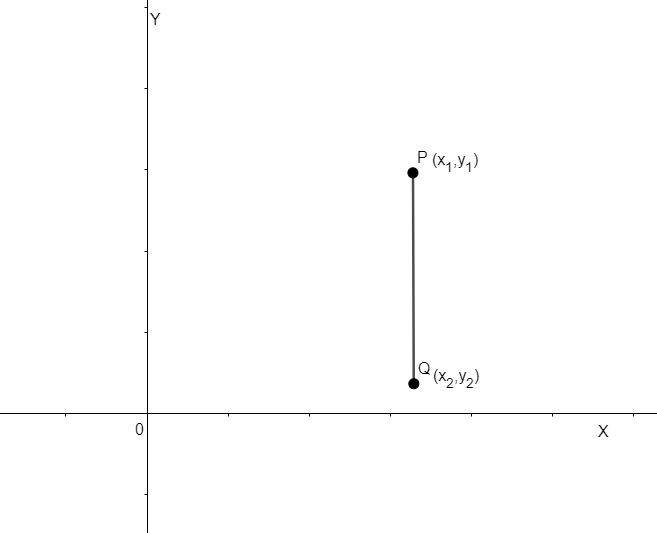
Now, we know that the equation of a line parallel to the y – axis is given as x = constant. So, we can say that the x – coordinate of points P and Q will be the same because the x – coordinate of any two points on the line PQ will remain constant. So, we have,
\[\Rightarrow {{x}_{1}}={{x}_{2}}.....\left( i \right)\]
Now, applying the distance formula given as \[PQ=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\] we get,
\[\Rightarrow PQ=\sqrt{{{\left( 0 \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\left[ \text{using relation (i)} \right]\]
\[\Rightarrow PQ=\sqrt{{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
\[\Rightarrow PQ=\left| {{y}_{2}}-{{y}_{1}} \right|\]
Here, the modulus sign is considered to keep the value of the distance positive.
(ii) When PQ is parallel to x-axis
In this case, one of the possible diagrams can be shown as

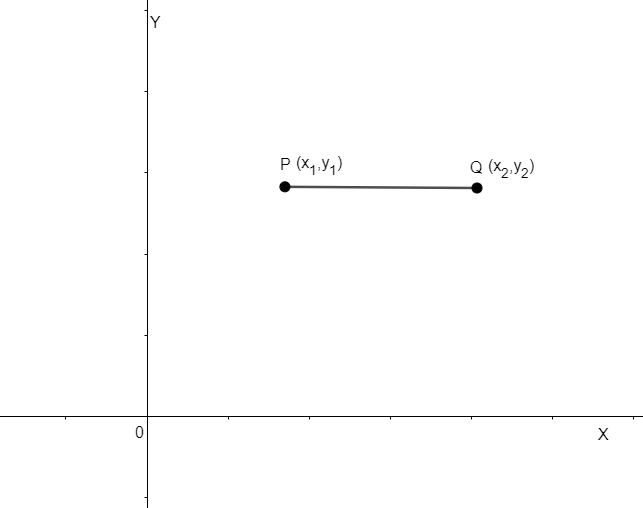
Now, we know that the equation of the line parallel to x – axis is given as y = constant. So, we can say that the y – coordinate of points P and Q will be the same because the y – coordinate of any two points on the line PQ will remain constant. So, we have,
\[\Rightarrow {{y}_{1}}={{y}_{2}}......\left( ii \right)\]
Now, applying the same distance formula, we get,
\[\Rightarrow PQ=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{0}^{2}}}\left[ \text{using equation (ii)} \right]\]
\[\Rightarrow PQ=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}}\]
\[\Rightarrow PQ=\left| {{x}_{2}}-{{x}_{1}} \right|\]
Here also the modulus sign is considered to keep the value of the distance positive.

Note:
 One must note that the significance of the modulus sign in the above answers. Actually, we have shown the line PQ in the first quadrant which is one of the possible conditions. P and Q may lie in other quadrants also. So, x and y – coordinates can be positive or negative depending on the situation. So, the difference \[\left( {{x}_{2}}-{{x}_{1}} \right)\] or \[\left( {{y}_{2}}-{{y}_{1}} \right)\] can be negative also but we know that the distance is a scalar quantity and cannot be negative. So, to keep the distance positive, a modulus sign is applied.