Question

How do you find the diameter of the sun given angular diameter and distance ?

Answer 1

Hint: The angular diameter of a spherical object determines its size to view from a particular distance. This angular diameter determines how small or big the object is from the viewer’s point. So we can say that the angular diameter changes from the viewer’s distance from the object.

Complete step by step answer:
(i) Imagine we people are seeing the sun from the earth’s surface. It appears in particular size. We think that the sun is in that size. But it is not. Our earth is \[1.5 \times {10^{11}}m\] away from the size. This distance affects our view on its size.We can imagine the triangle for this picture.

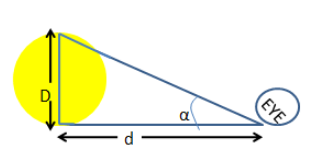
(ii) This picture gives us a right angled triangle. The angle\[\alpha \]is the angular diameter. The D is the diameter of the sun and d is the distance between the observer and the object.
(iii) On considering the right angled triangle here,
\[\tan \alpha = \dfrac{D}{d}\]
\[ \therefore D = d.\tan \alpha \]
Hence we can find the diameter of the sun by just knowing the distance between the observer from the sun and the angular diameter.

Additional information:
(i) The angular diameter is said to be\[0.54^\circ \]. We know that the earth is \[1.5 \times {10^{11}}m\]. This is taken as d. The diameter of the sun is estimated as \[1.4 \times {10^9}m\].
On applying these values gives,
\[\alpha = {\tan ^{ - 1}}\left[ {\dfrac{{1.4 \times {{10}^9}}}{{1.5 \times {{10}^{11}}}}} \right]\]
\[ \Rightarrow \alpha = 0.54^\circ \]
(ii) When we see the sun and moon from the earth, both seem the same size. But it is not. The sun’s diameter is 400 times larger than the moon. But it looks the same size because the sun is 400 times apart from the earth than the moon.

Note:The angular diameter helps physicists to know the actual size of the planet. It helps to know how far the planet is away from the sun. The angular diameter can be found by the diameter and the distance. And the diameter of any spherical object also can be found by the angular diameter and the distance.