Questions & Answers
Question
Answers
Related Questions
Find the diagonal of a square whose side is \[10cm\].
Answer
![Verified]()
Verified
Verified
Hint:As we know the side of the given square is \[10cm\]. And in a square, all the four sides are equal to each other as well as all the sides interest to its adjacent side at \[{90^0}\]. Therefore, the figure formed by joining the two opposite vertices of a square, is a right-angled triangle with two equal sides.
Complete step-by- step solution:
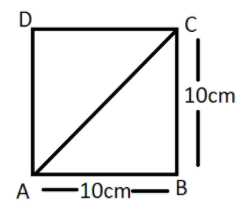
Given that Side of the square is \[10cm\]
In right angled\[\vartriangle ABC\]
Using Pythagoras theorem
\[A{B^2} + B{C^2} = A{C^2}\] \[\left[ {Bas{e^2} + Perpendicular{r^2} = Hypotenuse{e^2}} \right]\]
As we know, the sides of a square are equal to each other.
$\Rightarrow$ \[AB = BC\]
$\Rightarrow$\[{10^2} + {10^2} = A{C^2}\]
$\Rightarrow$\[100 + 100 = A{C^2}\]
$\Rightarrow$\[200 = A{C^2}\]
$\Rightarrow$\[AC = \sqrt {200} \]
$\Rightarrow$\[AC = \sqrt {2 \times 2 \times 2 \times 5 \times 5} \]
$\Rightarrow$\[AC = 2 \times 5\sqrt 2 \]
$\Rightarrow$\[AC = 10\sqrt 2 \]
Therefore, the diagonal of square will be \[10\sqrt 2 \]
Note: A square can have two diagonals. Each of the diagonal can be formed by joining the diagonally opposite vertices of a square. The properties of diagonals are as follows-
Both the diagonals are congruent (same length). Both the diagonals bisect each other, i.e. the point of joining of the two diagonals is the midpoint of both the diagonals. A diagonal divides a square into two isosceles right-angled triangles. The sum of all the internal angles of a square is equal to \[360 \circ \]and a square is a regular quadrilateral that has four equal sides and four same angles.
The diagonal of a square with side ‘a’ can be calculated using a formula \[a\sqrt 2 \]. Remember, both the diagonals of a square are equal to each other.
Complete step-by- step solution:
Given that Side of the square is \[10cm\]
In right angled\[\vartriangle ABC\]
Using Pythagoras theorem
\[A{B^2} + B{C^2} = A{C^2}\] \[\left[ {Bas{e^2} + Perpendicular{r^2} = Hypotenuse{e^2}} \right]\]
As we know, the sides of a square are equal to each other.
$\Rightarrow$ \[AB = BC\]
$\Rightarrow$\[{10^2} + {10^2} = A{C^2}\]
$\Rightarrow$\[100 + 100 = A{C^2}\]
$\Rightarrow$\[200 = A{C^2}\]
$\Rightarrow$\[AC = \sqrt {200} \]
$\Rightarrow$\[AC = \sqrt {2 \times 2 \times 2 \times 5 \times 5} \]
$\Rightarrow$\[AC = 2 \times 5\sqrt 2 \]
$\Rightarrow$\[AC = 10\sqrt 2 \]
Therefore, the diagonal of square will be \[10\sqrt 2 \]
Note: A square can have two diagonals. Each of the diagonal can be formed by joining the diagonally opposite vertices of a square. The properties of diagonals are as follows-
Both the diagonals are congruent (same length). Both the diagonals bisect each other, i.e. the point of joining of the two diagonals is the midpoint of both the diagonals. A diagonal divides a square into two isosceles right-angled triangles. The sum of all the internal angles of a square is equal to \[360 \circ \]and a square is a regular quadrilateral that has four equal sides and four same angles.
The diagonal of a square with side ‘a’ can be calculated using a formula \[a\sqrt 2 \]. Remember, both the diagonals of a square are equal to each other.
×
Sorry!, This page is not available for now to bookmark.
Like this
Liked
-
LIVECourses
-
Crash Courses 2021
-
Vedantu Pro
-
Vedantu Assist
-
Class 12
-
-
JEE
-
JEE Main & Advanced 2021
-
JEE Main & Advanced 2022
-
-
NEET
-
NEET 2021
-
NEET 2022
-
-
NDA
-
CBSE
-
Commerce
-
Class 11
-
Class 12
-
-
ICSE
-
Maharashtra Board
-
Class 9
-
Class 10
-
-
Micro Courses
-
-
FREEMaster Classes
-
PREMIUM1-on-1 Classes
-
Study Material
-
NCERT Solutions
-
Previous Year Papers
-
Mock Tests
-
Sample Papers
-
Reference Book Solutions
-
ICSE Solutions
-
School Syllabus
-
Revision Notes
-
Important Questions
-
Math Formula Sheets
-
-
More
Book your FREE Online counselling session
Share your contact information
Your FREE Online counselling session has been booked!
Vedantu academic counsellor will be calling you shortly for your Online Counselling session.
DONE
Please try again later
OK
NCERT Book Solutions
Reference Book Solutions
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
(Mon-Sun: 9am - 11pm IST)
Questions?
Chat with us
