Question

Find the diagonal of a rectangle whose length is 35 cm and breadth is 12 cm.

Answer 1

Hint: To solve this question first we need to know that any two alternate sides of a rectangle bisects each other at right angle i.e. $ {{90}^{\circ }} $ so we can apply the Pythagoras theorem in the triangle formed by a diagonal and two alternate sides of the rectangle. Pythagoras theorem states that in a right angled triangle, $ {{(hypotenuse)}^{2}}={{(base)}^{2}}+{{(height)}^{2}} $ , so we can find the length of the diagonal from the above formula by taking hypotenuse as diagonal and length and breadth of rectangle as base and height respectively.

Complete step-by-step answer:
We are given that,
Length of the rectangle is equal to 35 cm, and
Breadth of the rectangle is equal to 12 cm.
First we need to draw a diagonal to the given rectangle.
So, suppose we have a rectangle ABCD and we draw the diagonal AC as,

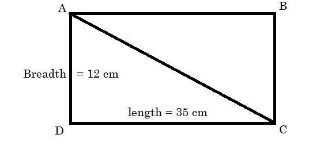
Now, we are supposed to find the length of AC,
To find it we can use Pythagoras theorem but, first let’s see what does it state,
It states that in a right angled triangle as shown below,

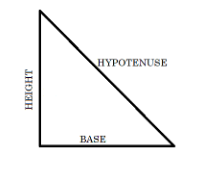
 $ {{(hypotenuse)}^{2}}={{(base)}^{2}}+{{(height)}^{2}} $
So we will apply this theorem in $ \Delta ACD $ of the rectangle to find out the value of AC ,
By applying the above theorem in $ \Delta ACD $ we will get,
 $ A{{C}^{2}}=A{{D}^{2}}+C{{D}^{2}} $,
 $ A{{C}^{2}}={{12}^{2}}+{{35}^{2}} $,
 $ A{{C}^{2}}=144+1225 $,
 $ A{{C}^{2}}=1369 $,
 $ AC=\sqrt{1369} $
 $ AC=37 $
Hence we get the length of diagonal of the rectangle as 37 cm.

Note: We can also solve for the value of diagonal BD in the rectangle by applying Pythagoras theorem in $ \Delta ABD $ but it does not matter which diagonal you use as we know that length of both of the diagonals of a rectangle are equal. Try to read out more properties of rectangles, squares, rhombus etc. it’ll help you solve these kinds of problems in future easily.