Question

Find the current in the three resistors in figure.

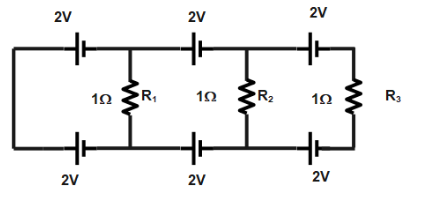
Answer 1

Hint:To solve circuit-based questions we have to know the concepts and applications of KVL and KCL. Name the ends of the circuits as ABCDEFGH. Let us consider a current $i$ coming out from the lower left most cell of the circuit AB and then dividing into ${i_1}$ and$i - {i_1}$ at point G. Now let ${i_1}$ be again divided into part ${i_1}$ and ${i_1} - {i_2}$ at the point F.

Complete step by step answer:

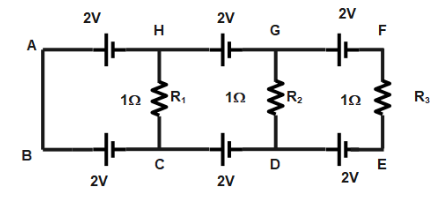
Considering loop AHGBA:
 $ 2 + (i - {i_1}) - 2 = 0 \\
\Rightarrow i - {i_1} = 0. \\
\Rightarrow 2 + (i - {i_1}) - 2 = 0 \\
\Rightarrow i - {i_1} = 0$
Thus $i = {i_1}$ . $ - - - - (1)$
Considering loop BGFCB:
$2 - (i - {i_1}) - 2 + {i_1} - {i_2} = 0$
$\Rightarrow (i - {i_1}) + {i_1} - {i_2} = 0 $
But we know that $i = {i_1}$ , hence the first term gets cancelled.
Thus, ${i_1} = {i_2}$ $ - - - - (2)$
Considering loop CFEDC, we get
$2 + {i_2} - ({i_1} - {i_2}) - 2 = 0 \\$
$\Rightarrow 2{i_2} - {i_1} = 0$ $ - - - - (3)$

Now compare equation 2 and equation 3, we see that the value is only possible when both ${i_1},{i_2}$ are zero. Thus we can also confirm that $i{\text{ = 0}}$.Now lets see the current through resistors:
For $R_1$: current is $i - {i_1}$ , but from (1) we see the value is zero. Hence current through $R_1$ is zero.
For $R_2$: current is ${i_1} - {i_2} = 0$, but from (2) we see the value is zero. Hence current through $R_2$ is zero. Similarly, for $R_3$ we see that the value of current through the resistance is zero.

Hence no current passes through these three resistances.

Additional information:KVL: The law which deals with the conservation of energy for a closed circuit path. The law states that for a closed loop path the algebraic sum of all the emf around any closed loop in a circuit is equal to zero.

Note: From these types of questions it is to be kept in mind that if equal and opposite emf are applied in a circuit, then no current flows through the circuit. Thus we can now apply this concept to other questions where there may be any number of resistances and emf.