Question

Find the current I in the following circuit.
      

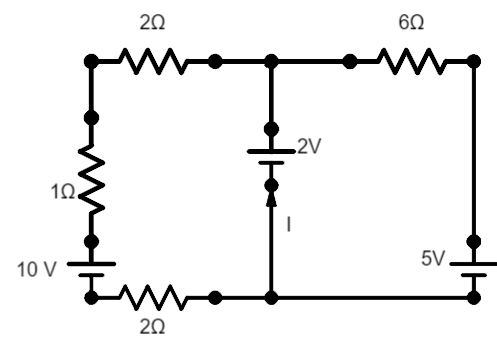
Answer 1

Hint: We need to understand the circuital laws which govern the electrical circuits in order to find the current through the arm indicated in a circuit. The current through the circuit is dependent on the Kirchhoff’s laws and the type of combination of resistors.

Complete answer:
We are given a circuit which consists of resistor and multiple voltage sources. We can see that there are two loops in the circuit which means we can apply the Kirchhoff’s loop rule or the voltage law to solve the given problem. According to Kirchhoff's loop rule the algebraic sum of the potential drops in the circuit will be equal to the emf provided in the circuit.
Let us consider the two loops given to us here.
We can find the sum total of the potential drops in the resistors by finding the product of the resistance of the resistor and the current through it as potential drop is given by the Ohm’s law as–
\[V=IR\]
     

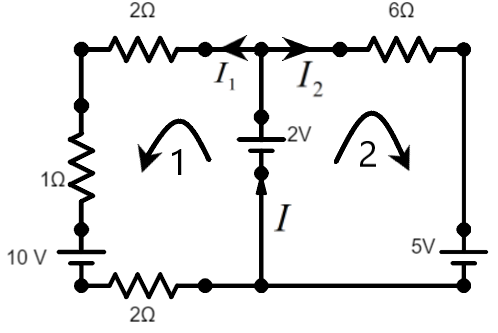
Now, consider loop 1. There are two emfs each of 10V and 2V in the loop which are in the opposite direction. The algebraic sum can be given as –
\[\begin{align}
  & {{\varepsilon }_{1}}+{{\varepsilon }_{2}}={{V}_{1}}+{{V}_{2}}+{{V}_{3}} \\
 & \Rightarrow -10+2={{I}_{1}}(2+1+2) \\
 & \Rightarrow {{I}_{1}}=\dfrac{5}{-8}A \\
 & \therefore {{I}_{1}}=-\dfrac{5}{8}A \\
\end{align}\]
Now, we can use the same technique in the loop 2 to get the current in that loop using the Kirchhoff’s loop as –
\[\begin{align}
  & {{\varepsilon }_{1}}+{{\varepsilon }_{2}}={{V}_{4}} \\
 & \Rightarrow 2-5=6{{I}_{2}} \\
 & \therefore {{I}_{2}}=-\dfrac{1}{2}A \\
\end{align}\]
We can see that the total current I will be the sum of the two currents. We can find the total current as –
\[\begin{align}
  & I={{I}_{1}}+{{I}_{2}} \\
 & \Rightarrow I=-\dfrac{5}{8}+-\dfrac{1}{2} \\
 & \therefore I=-1.125A \\
\end{align}\]
The total current will be 1.125A along the opposite direction indicated by the arrow of I.
This is the required solution.

Note:
We need to keep in mind that the current in a series combination of resistors will be constant. We used that idea to consider the current through each of the resistors in each of the loops to be equal and thus the sum of them to the total current in the circuit.