
Find the cube root of 15625 by prime factorisation method.
Answer
508k+ views
Hint: Here, to find the cube root of 15625 we can use the method of prime factorisation. In prime factorisation we factorise the numbers into prime numbers, called as prime factors. After doing a prime factorisation group the factors in three such that each member of the group is the same. Take one factor from each group and then multiply to obtain the cube root.
Complete step-by-step solution -
Here, we have to find the cube root of 15625.
First let us discuss the cube root. The cube root of a number is a special value that, when used in multiplication three times gives that number. That is, if ‘$a$’ is the cube root of $x$ then we can write $x={{a}^{3}}=a\times a\times a$.
Now, we have to apply the prime factorisation method to find the cube root 15625.
In prime factorisation we factorise the numbers into prime numbers, called as prime factors. There are two methods of prime factorisation.
Division method
Factor tree method
Here, we are applying the division method. In the division method of prime factorisation, we have to follow certain steps. They are:
First we divide the number by the smallest prime number which divides the number exactly.
We divide the quotient again by the smallest prime number, or the next smallest prime number, if it is not exactly divisible by the smallest prime number. Repeat the process again and again till the quotient becomes 1. Here we are using only prime numbers to divide.
We multiply all the prime factors, where the product is the number itself.
Therefore, for finding cube root by prime factorisation we have to group the factors in three such that each number of the group is the same. Take one factor from each group and then multiply to obtain the cube root.
Now, consider the prime factorisation:
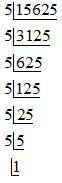
Next, we can express 15625 as the product of prime factors, we will get:
$15625=5\times 5\times 5\times 5\times 5\times 5$
In the next step we have to group the numbers in three with the same numbers in one group. Hence, we obtain:
$15625=(5\times 5\times 5)\times (5\times 5\times 5)$
Now, take the cube root of 15625, then take one factor from each group we get:
$\sqrt[3]{15625}=5\times 5$
Next, we have to multiply the factors to get the cube root of 15625. Hence we will get:
$\sqrt[3]{15625}=25$
Hence, we can say that 15625 is a perfect cube.
Therefore, the required cube root of 15625 is 25.
Note: Here, after prime factorisation, you will get prime factors. Now, to obtain the cube root, take the similar numbers in groups of three and one factor from each group should be taken and then multiply all such factors. Here, there are 6 prime factors and every factor is 5. So we grouped them in three, you will get 2 groups and take one 5 from each group and multiply both the factors, we will get 25 as the cube root. While doing the prime factorisation, always begin the division with the smallest prime number which can divide the number.
Complete step-by-step solution -
Here, we have to find the cube root of 15625.
First let us discuss the cube root. The cube root of a number is a special value that, when used in multiplication three times gives that number. That is, if ‘$a$’ is the cube root of $x$ then we can write $x={{a}^{3}}=a\times a\times a$.
Now, we have to apply the prime factorisation method to find the cube root 15625.
In prime factorisation we factorise the numbers into prime numbers, called as prime factors. There are two methods of prime factorisation.
Division method
Factor tree method
Here, we are applying the division method. In the division method of prime factorisation, we have to follow certain steps. They are:
First we divide the number by the smallest prime number which divides the number exactly.
We divide the quotient again by the smallest prime number, or the next smallest prime number, if it is not exactly divisible by the smallest prime number. Repeat the process again and again till the quotient becomes 1. Here we are using only prime numbers to divide.
We multiply all the prime factors, where the product is the number itself.
Therefore, for finding cube root by prime factorisation we have to group the factors in three such that each number of the group is the same. Take one factor from each group and then multiply to obtain the cube root.
Now, consider the prime factorisation:
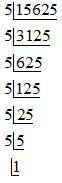
Next, we can express 15625 as the product of prime factors, we will get:
$15625=5\times 5\times 5\times 5\times 5\times 5$
In the next step we have to group the numbers in three with the same numbers in one group. Hence, we obtain:
$15625=(5\times 5\times 5)\times (5\times 5\times 5)$
Now, take the cube root of 15625, then take one factor from each group we get:
$\sqrt[3]{15625}=5\times 5$
Next, we have to multiply the factors to get the cube root of 15625. Hence we will get:
$\sqrt[3]{15625}=25$
Hence, we can say that 15625 is a perfect cube.
Therefore, the required cube root of 15625 is 25.
Note: Here, after prime factorisation, you will get prime factors. Now, to obtain the cube root, take the similar numbers in groups of three and one factor from each group should be taken and then multiply all such factors. Here, there are 6 prime factors and every factor is 5. So we grouped them in three, you will get 2 groups and take one 5 from each group and multiply both the factors, we will get 25 as the cube root. While doing the prime factorisation, always begin the division with the smallest prime number which can divide the number.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 English: Engaging Questions & Answers for Success

Why are manures considered better than fertilizers class 11 biology CBSE

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What is the difference between rai and mustard see class 8 biology CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE




