Question

How do you find the critical numbers for \[g\left( t \right) = \left| {3t - 4} \right|\] to determine the maximum and minimum?

Answer 1

Hint: In the above question, we are given a function of \[t\] as \[g\left( t \right) = \left| {3t - 4} \right|\] . We have to find the critical numbers to determine the maximum and minimum of the given function. Critical points of a function are those points for which the value of the derivative of the function is either zero or undefined. First we have to find the derivative of \[g\left( t \right)\] that is \[g'\left( t \right)\] and then put \[g\left( t \right) = 0\] to find the critical point \[{t_0}\] .

Complete step-by-step answer:
Given function is
\[ \Rightarrow g\left( t \right) = \left| {3t - 4} \right|\]
We have to find its critical points to determine the maximum and minimum.
Since, \[g\left( t \right) = \left| {3t - 4} \right|\] , hence we can also write it in the form
\[ \Rightarrow g\left( t \right) = \left| {3t - 4} \right|\]
Or,
\[ \Rightarrow g\left( t \right) = \left\{ \begin{gathered}
  3t - 4,{\text{if }}t \geqslant \dfrac{4}{3} \\
  4 - 3t,{\text{if }}t < \dfrac{4}{3} \\
\end{gathered} \right.\]
Now, differentiating the function \[g\left( t \right)\] once with respect to \[t\] , we get
\[ \Rightarrow g'\left( t \right) = \left\{ \begin{gathered}
  3,{\text{if }}t > \dfrac{4}{3} \\
   - 3,{\text{if }}t < \dfrac{4}{3} \\
\end{gathered} \right.\]
Now, note that the derivative \[g'\left( t \right)\] is either \[3\] or \[ - 3\] for the values \[t > \dfrac{4}{3}\] and \[t < \dfrac{4}{3}\] but it is not defined for the value \[t = \dfrac{4}{3}\] .
Hence, \[g'\left( t \right)\] is never equal to zero and also \[g'\left( t \right)\] is not differentiable at \[t = \dfrac{4}{3}\] .
Hence, here \[t = \dfrac{4}{3}\] is the only critical point for the function \[g\left( t \right) = \left| {3t - 4} \right|\] .
That means the function \[g\left( t \right)\] has either minima or maxima on the point \[t = \dfrac{4}{3}\] .
Also the function is a modulus function, hence it is always non-negative.
Therefore, it will be minimum only when \[g\left( t \right) = 0\] at \[t = \dfrac{4}{3}\] .
We can observe that the function \[g\left( t \right)\] is decreasing on the left of \[t = \dfrac{4}{3}\] and increasing on the right of \[t = \dfrac{4}{3}\] .
Therefore, \[g\left( t \right)\] has local minima at \[t = \dfrac{4}{3}\] .
The minimum value is given by \[g\left( {\dfrac{4}{3}} \right)\] that is \[0\] .
Hence, \[g\left( {\dfrac{4}{3}} \right) = 0\] is the local minima of \[g\left( t \right) = \left| {3t - 4} \right|\] at the critical point \[t = \dfrac{4}{3}\] .

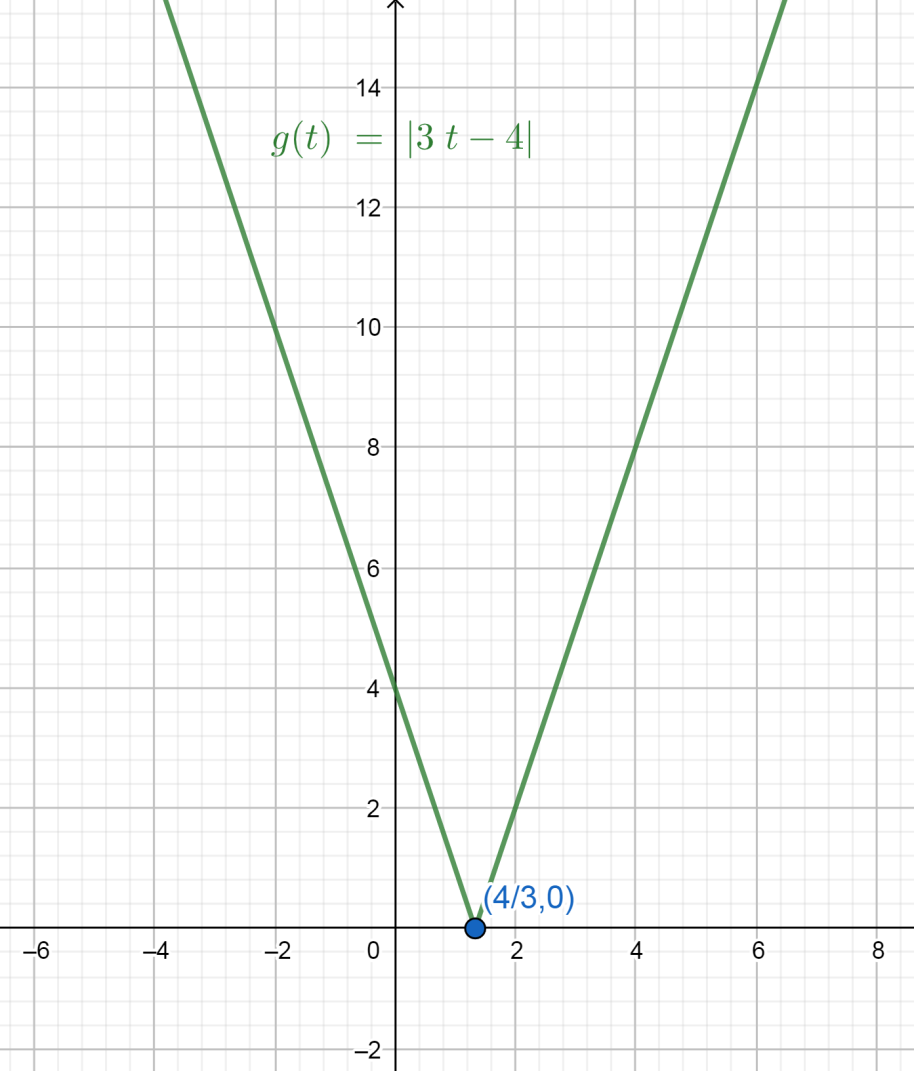
Note: We can also draw the graph for the function \[g\left( t \right) = \left| {3t - 4} \right|\] to see the increasing and decreasing nature of the function. Here, we can note that the function has the minimum value at \[t = \dfrac{4}{3}\] .

The first derivative of a point is the slope of the tangent line at that point. When the slope of the tangent line is 0, the point is either a local minimum or a local maximum. Thus when the first derivative of a point is 0, the point is the location of a local minimum or maximum. The function either has local minima or local maxima at the critical point \[{x_0}\] . If then it has local maxima at \[{x_0}\] and if then the function has local minima at the critical point \[{x_0}\] .