Question

How do you find the coterminal with angle $-{{135}^{\circ }}$ ?

Answer 1

Hint: We are given an angle as $-{{135}^{\circ }}$ , we are asked to find the coterminal with the angle $-{{135}^{\circ }}$ , to do so we will learn about coterminal angles, we will see how they are defined graphically, we will work with some example, then we will check how many coterminal angles we can find in general. After that we will work on our problem to find coterminal angle with the angle $-{{135}^{\circ }}$ .

Complete step by step answer:
We are given an angle as $-{{135}^{\circ }}$ , we are asked to find the angle coterminal with the $-{{135}^{\circ }}$ angle, to do so we will learn what does coterminal angles.
Coterminal angles are angles in standard position that mean angles with the initial side on the positive x-axis and have the common terminal side.
For example ${{30}^{\circ }}$ and $-{{330}^{\circ }}$ .
If we sketch them on graph, we get better understanding

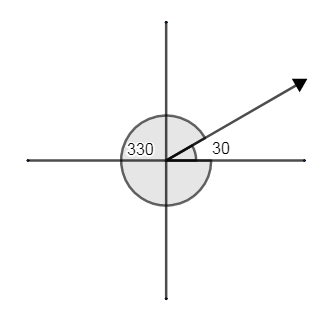
Here ${{30}^{\circ }}$ and $-{{330}^{\circ }}$ start from the positive axis, and have a common terminal.
So, they are coterminal angles by definition.
They can be more than 1 coterminal angle for any given angle, like for 30, apart from -330 degree, we have 390degree.

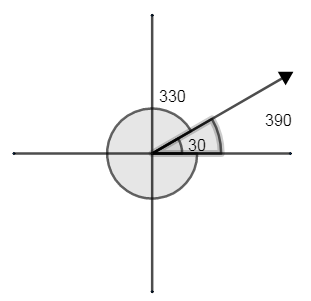
In general, if $\theta $ is any angle whose initial side is positive x-axis then $\theta +n\left( {{360}^{\circ }} \right)$ is coterminal angle with $\theta $ where ‘n’ is non zero integer.
Now we work on our problem, we are asked to find the coterminal angle with the angle $-{{135}^{\circ }}$ .
So, we consider $\theta $ as $-{{135}^{\circ }}$
We use this to find a coterminal angle.
As for angle $\theta $ , co terminal is given as $\theta +n\left( {{360}^{\circ }} \right)$ .
So, for $\theta =-{{135}^{\circ }}$ co terminal is given as –
$-{{135}^{\circ }}+n\left( {{360}^{\circ }} \right)$ .
We put $n=1$ , we get –
$\Rightarrow -{{135}^{\circ }}+1\times 360$ .
By simplifying, we get –
$\begin{align}
  & =-{{135}^{\circ }}+{{360}^{\circ }} \\
 & =225 \\
\end{align}$

Note:
As we change the value of ‘n’, we can find more than 1 angle which is coterminal with $-{{135}^{\circ }}$ .
Remember that positive or negative sign in the angle is regard to the orientation, if we measure angle in clockwise direction this it is negative, if we measure anti-clock wise then it is positive also graph way to find coterminal angle is also strong as we can clearly see whether condition of being coterminal angle are satisfied or not.