Answer
Verified441.6k+ views
Hint: Here in this question, the cot function is given. Cot is a derived function from the basic trigonometric functions like tangent (tan). We can represent cot function in the form of sine and cosine as $\dfrac{\cos \theta }{\sin \theta }$. And, by using trigonometric ratios we have to find the cot of a 68-degree angle i.e. $\cot {{68}^{\circ }}$. So, we should know about the trigonometric ratios for different angles.
Let’s see some basic trigonometric functions:
$\Rightarrow $ Sine (sin)
$\Rightarrow $Cosine (cos)
$\Rightarrow $Tangent (tan)
When we say $\cot \theta $, here $\theta $ means angle in degrees.
Derived functions that are derived from basic trigonometric functions are:
$\Rightarrow $cosec$\theta $ = $\dfrac{1}{\sin \theta }$
$\Rightarrow $sec$\theta $ = $\dfrac{1}{\cos \theta }$
$\Rightarrow $tan$\theta $ = $\dfrac{\sin \theta }{\cos \theta }$ = $\dfrac{1}{\cot \theta }$
$\Rightarrow $cot$\theta $ = $\dfrac{1}{\tan \theta }$ = $\dfrac{\cos \theta }{\sin \theta }$
You know what cot$\theta $ is! Let’s find out.
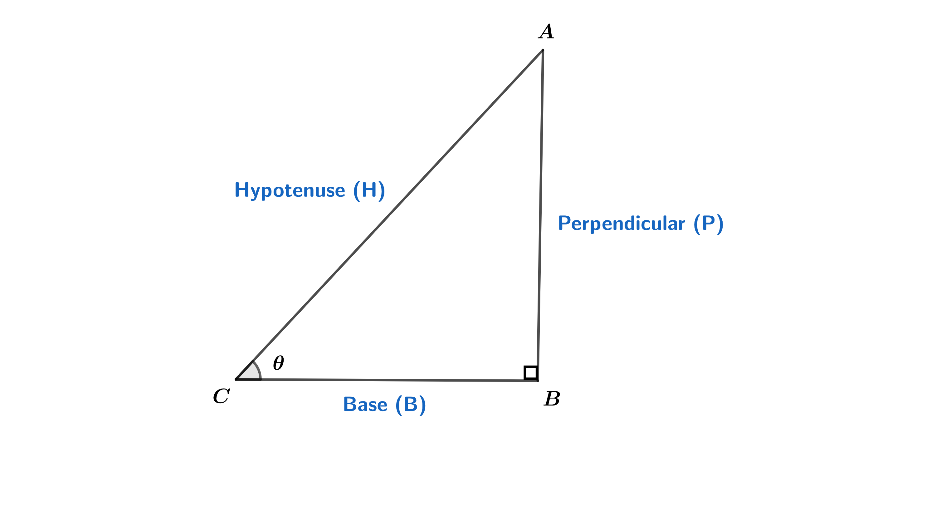
So, from the figure,
$\Rightarrow $sin$\theta $ = $\dfrac{perpendicular(P)}{hypotenuse(H)}$
$\Rightarrow $cos$\theta $ = \[\dfrac{base(B)}{hypotenuse(H)}\]
And we know that cot$\theta $ = $\dfrac{\cos \theta }{\sin \theta }$
So, cot$\theta $ = \[\dfrac{base(B)}{perpendicular(P)}\]
Now, let’s have a look at some even and odd functions as well.
$\Rightarrow $sin(-x) = -sinx
$\Rightarrow $ cos(-x) = cosx
$\Rightarrow $ tan(-x) = -tanx
$\Rightarrow $ cot(-x) = -cotx
$\Rightarrow $ cosec(-x) = -cosecx
$\Rightarrow $sec(-x) = secx
Now, let’s make a table of trigonometric ratios for basic trigonometric functions i.e. sin, cos, tan, cot, sec, and cosec.
We should also know what the graph of cotx looks like.
As we know that
cot$\theta $ = $\dfrac{1}{\tan \theta }$
So,
cot${{68}^{\circ }}$ = $\dfrac{1}{\tan {{68}^{\circ }}}$
So, cot${{68}^{\circ }}$ = \[\dfrac{1}{\tan {{68}^{\circ }}}\] = \[\dfrac{1}{2.475}\]
$\therefore \cot {{68}^{\circ }}=$ 0.40
Note:
You should remember all the functions and trigonometric ratios before solving any question related to trigonometry. As cot$\theta $ is a derived function, so you should also know the basic function of cot i.e. tan$\theta $ and how to derive the cot$\theta $. Find the exact value of the degree using the functions. Don’t keep the value up to 2 decimal places while calculating $\tan {{68}^{\circ }}$.
Let’s see some basic trigonometric functions:
$\Rightarrow $ Sine (sin)
$\Rightarrow $Cosine (cos)
$\Rightarrow $Tangent (tan)
When we say $\cot \theta $, here $\theta $ means angle in degrees.
Derived functions that are derived from basic trigonometric functions are:
$\Rightarrow $cosec$\theta $ = $\dfrac{1}{\sin \theta }$
$\Rightarrow $sec$\theta $ = $\dfrac{1}{\cos \theta }$
$\Rightarrow $tan$\theta $ = $\dfrac{\sin \theta }{\cos \theta }$ = $\dfrac{1}{\cot \theta }$
$\Rightarrow $cot$\theta $ = $\dfrac{1}{\tan \theta }$ = $\dfrac{\cos \theta }{\sin \theta }$
You know what cot$\theta $ is! Let’s find out.
So, from the figure,
$\Rightarrow $sin$\theta $ = $\dfrac{perpendicular(P)}{hypotenuse(H)}$
$\Rightarrow $cos$\theta $ = \[\dfrac{base(B)}{hypotenuse(H)}\]
And we know that cot$\theta $ = $\dfrac{\cos \theta }{\sin \theta }$
So, cot$\theta $ = \[\dfrac{base(B)}{perpendicular(P)}\]
Now, let’s have a look at some even and odd functions as well.
$\Rightarrow $sin(-x) = -sinx
$\Rightarrow $ cos(-x) = cosx
$\Rightarrow $ tan(-x) = -tanx
$\Rightarrow $ cot(-x) = -cotx
$\Rightarrow $ cosec(-x) = -cosecx
$\Rightarrow $sec(-x) = secx
Now, let’s make a table of trigonometric ratios for basic trigonometric functions i.e. sin, cos, tan, cot, sec, and cosec.
| Trigonometric ratios(angle $\theta $ in degrees) | ${{0}^{\circ }}$ | ${{30}^{\circ }}$ | ${{45}^{\circ }}$ | ${{60}^{\circ }}$ | ${{90}^{\circ }}$ |
| sin$\theta $ | 0 | $\dfrac{1}{2}$ | $\dfrac{1}{\sqrt{2}}$ | $\dfrac{\sqrt{3}}{2}$ | 1 |
| cos$\theta $ | 1 | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{1}{\sqrt{2}}$ | $\dfrac{1}{2}$ | 0 |
| tan$\theta $ | 0 | $\dfrac{1}{\sqrt{3}}$ | 1 | $\sqrt{3}$ | $\infty $ |
| cosec$\theta $ | $\infty $ | 2 | $\sqrt{2}$ | $\dfrac{2}{\sqrt{3}}$ | 1 |
| sec$\theta $ | 1 | $\dfrac{2}{\sqrt{3}}$ | $\sqrt{2}$ | 2 | $\infty $ |
| cot$\theta $ | $\infty $ | $\sqrt{3}$ | 1 | $\dfrac{1}{\sqrt{3}}$ | 0 |
We should also know what the graph of cotx looks like.
As we know that
cot$\theta $ = $\dfrac{1}{\tan \theta }$
So,
cot${{68}^{\circ }}$ = $\dfrac{1}{\tan {{68}^{\circ }}}$
So, cot${{68}^{\circ }}$ = \[\dfrac{1}{\tan {{68}^{\circ }}}\] = \[\dfrac{1}{2.475}\]
$\therefore \cot {{68}^{\circ }}=$ 0.40
Note:
You should remember all the functions and trigonometric ratios before solving any question related to trigonometry. As cot$\theta $ is a derived function, so you should also know the basic function of cot i.e. tan$\theta $ and how to derive the cot$\theta $. Find the exact value of the degree using the functions. Don’t keep the value up to 2 decimal places while calculating $\tan {{68}^{\circ }}$.