Question

Find the cost of fencing a rectangular park of length 350 m and breadth 250 m at the rate of 18.50 rupees per meter.

Answer 1

Hint: Rectangle is a two-dimensional figure. It is a quadrilateral whose opposite sides are equal.
The angle between the two adjacent sides of the rectangle is ${90^ \circ }$.

Figure: Rectangle ABCD
Fencing is done along the boundary of the field.
Boundary implies the perimeter of the field.
The given field is rectangular. Thus using the formula of the perimeter of the rectangle, find the length of fencing.
The cost of the fencing can be calculated using the unitary method.
The unitary method is a technique for solving a problem by first finding the value of a single unit, and then finding the necessary value by multiplying the single unit value.

Complete step-by-step answer:
Step 1: Draw the given rectangle.

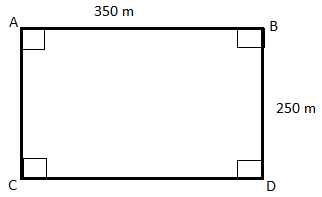
Figure: Given rectangle ABCD
Step 2: Given that:
The length of the rectangle ABCD = 350 m
The breadth of the rectangle ABCD = 250 m
Side AB and CD are the lengths of rectangle ABCD,
I.e. AB = CD
Side BC and AD are breadths of rectangle ABCD
I.e. BC = AD
Step 3: Find the length of fencing.
We know that for the length of fencing around the rectangle ABCD we have to calculate the perimeter of the rectangle ABCD.
The perimeter of a rectangle is two times the sum of its length and breadth.
Perimeter of rectangle $ = 2({\text{length + breadth}}){\text{ }}units$
Perimeter of rectangle $ = 2({\text{AB + BC}}){\text{ m}}$
                                           $
   = 2\left( {350 + 250} \right){\text{ }}m \\
   = 2 \times 600{\text{ m}} \\
   = 1200{\text{ m}} \\
 $
Thus, the length of the fencing of rectangle ABCD is 1,200 m.
Step 4: Find the cost of fencing.
Given that Rate of fencing per meter $ = 18.50{\text{ rupees}}$
Length of fencing of rectangle ABCD = 1200 m
Cost of fencing of rectangle ABCD \[ = {\text{ length of fencing }} \times {\text{ rate of fencing per meter}}\]
                                                              $
   = 1200 \times 18.50{\text{ rupees}} \\
   = 22200{\text{ rupees}} \\
 $

The cost of fencing a rectangular park of length 350 m and breadth 250 m is 22,200 rupees.

Note: If the rectangular park is covered by grass then the area of the park should be calculated.
The area of the rectangle is the product of the length and breadth of the rectangle.
Area of rectangle $ = \left( {{\text{length }} \times {\text{ breadth}}} \right)sq.units$
Students get confused between the rectangle and parallelogram.
In a parallelogram, the angle between two adjacent sides are not equal to ${90^ \circ }$.

Figure: Parallelogram ABCD
The length of diagonals of a rectangle are equal which is not equal in the case of a parallelogram.