Question

Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
A. \[P\left( -2,{}^{-5}/{}_{-3} \right)\]
B. \[P\left( 2,{}^{-5}/{}_{3} \right)\]
C. \[Q\left( 0,{}^{-7}/{}_{3} \right)\]
D. \[Q\left( 0,{}^{7}/{}_{3} \right)\]

Answer 1

Hint: As it is the point of trisection, it divides the line into 3 parts, i.e. two points in AB line are P and Q. Find the ratio in which P and Q divides AB and use the trisection formula to get points P and Q.

Complete step-by-step answer:


Let the given points be A (4, -1) and B (-2, 3). Let P and Q be the two points in AB such that,
AP = PQ = QB.

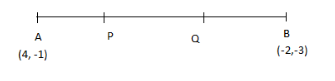
It is said that it’s in trisection, which means that the 2 points P and Q divide AB into 3 equal parts.
Let us consider AP = PQ = QB = m.
Point P divides AP and PB in the ratio, AP = m.
PB = PQ + QB = m + m = 2m.
\[\therefore AP:PB\Rightarrow m:2m=1:2.\]
Thus point P divides AP and PB in the ratio 1:2, i.e. P divides AB in the ratio 1:2.
Now let us find the value of P.
Let us take P(x, y)

The ratio is 1:2, thus \[{{m}_{1}}:{{m}_{2}}\]
\[{{m}_{1}}=1,{{m}_{2}}=2\].
The formula for finding the value of x and y with ratio is,
\[x=\dfrac{{{m}_{1}}{{x}_{2}}+{{m}_{2}}{{x}_{1}}}{{{m}_{1}}+{{m}_{1}}}\] and \[y=\dfrac{{{m}_{1}}{{y}_{2}}+{{m}_{2}}{{y}_{1}}}{{{m}_{1}}+{{m}_{2}}}.........(1)\]
Here \[\left( {{x}_{1}},{{y}_{1}} \right)=(4,-1)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)=(-2,-3)\].
Thus let us substitute these values and get x and y.
\[x=\dfrac{{{m}_{1}}{{x}_{2}}+{{m}_{2}}{{x}_{1}}}{{{m}_{1}}+{{m}_{1}}}=\dfrac{\left( 1\times -2 \right)+\left( 2\times 4 \right)}{1+2}=\dfrac{-2+8}{3}=\dfrac{6}{3}=2.\]
\[y=\dfrac{{{m}_{1}}{{y}_{2}}+{{m}_{2}}{{y}_{1}}}{{{m}_{1}}+{{m}_{2}}}=\dfrac{\left( 1\times -3 \right)+\left( 2\times -1 \right)}{1+2}=\dfrac{-3-2}{3}=\dfrac{-5}{3}.\]
Thus we got x = 2 and y = \[\dfrac{-5}{3}\].
Therefore we got point \[P\left( 2,{}^{-5}/{}_{3} \right)\].
Similarly point Q divides AB in the ratio of AQ and QB.

AQ = AP + PQ = m + m = 2m
and QB = m.
AQ:QB = 2m:m = 2:1.
So point Q divides AB in the ratio 2:1.
Now let us find the coordinates of Q.
Let us take Q (x, y), \[2:1={{m}_{1}}+{{m}_{2}}\].
\[{{m}_{1}}=2\] and \[{{m}_{2}}=1\].
Let us put values in the equation (1) to get values of x and y.
\[x=\dfrac{{{m}_{1}}{{x}_{2}}+{{m}_{2}}{{x}_{1}}}{{{m}_{1}}+{{m}_{1}}}=\dfrac{\left( 2\times -2 \right)+\left( 1\times 4 \right)}{2+1}=\dfrac{-4+4}{3}=\dfrac{0}{3}=0.\]
\[y=\dfrac{{{m}_{1}}{{y}_{2}}+{{m}_{2}}{{y}_{1}}}{{{m}_{1}}+{{m}_{2}}}=\dfrac{\left( 2\times -3 \right)+\left( 1\times -1 \right)}{2+1}=\dfrac{-6-1}{3}=\dfrac{-7}{3}.\]
Thus we got x = 0and y = \[\dfrac{-7}{3}\].
Thus we got point \[Q\left( 0,{}^{-7}/{}_{3} \right)\].
Thus we got the coordinates of points of trisection as \[P\left( 2,{}^{-5}/{}_{3} \right)\] and \[Q\left( 0,{}^{-7}/{}_{3} \right)\].
Option B and C are correct.

Note: If points P and Q which lie on the line segment AB divides it into 3 equal parts that means, if AP = PQ = QB, then the points P and Q are called Points of Trisection of AB. You have to remember that P divides AB in the ratio 1:2 and Q divides AB in the ratio 2:1.