Question

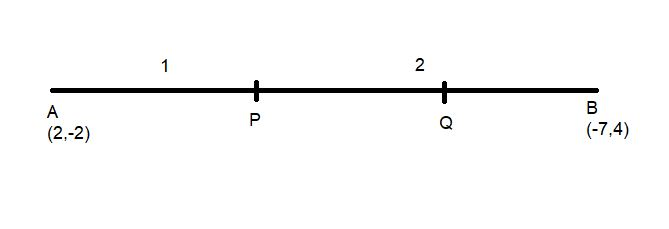
Find the coordinates of the points of trisection of the line segment joining the points A (2,-2) and B (-7, 4).

Answer 1

Hint: To solve this question first draw a line segment joining A and B and divide this line segment in three equal parts using point P and Q. We have to find P and Q using section formulae.

Complete step-by-step answer:
Let the given points be A ( 2, -2 ) and B ( -7 ,4 )
P and Q are two points on AB such that
AP = PQ = QB
Let k = AP = PQ = QB
Hence comparing AP and PB
AP = k
PB = PQ + QB = k + k = 2k
Hence, ratio of AP and PB = $\dfrac{m}{{2m}} = \dfrac{1}{2}$
Thus P divides AB in the ratio 1:2
Now let P (x,y)
Hence, ${m_1} = 1,{m_2} = 2$
And for AB
$
  {x_1} = 2,{x_2} = - 2 \\
  {y_1} = - 7,{y_2} = 4 \\
$
$x = \dfrac{{{m_1}{x_2} + {m_2}{x_1}}}{{{m_1} + {m_2}}} = \dfrac{{1 \times \left( { - 7} \right) + 2 \times 2}}{{1 + 2}} = \dfrac{{ - 7 + 4}}{3} = - 1$
$y = \dfrac{{{m_1}{y_2} + {m_2}{y_1}}}{{{m_1} + {m_2}}} = \dfrac{{1 \times 4 + 2 \times \left( { - 2} \right)}}{{1 + 2}} = \dfrac{{4 - 4}}{3} = 0$
Hence, point P is P ( -1, 0 )
Similarly,
Point Q divides AB in the ratio QA and QB
$ = \dfrac{{{\text{AQ}}}}{{{\text{QB}}}}$
$
   = \dfrac{{{\text{AP + PQ}}}}{{{\text{QB}}}} = \dfrac{{K + K}}{K} = \dfrac{2}{1} \\
   = 2:1 \\
 $
Now we have to find Q.
Let Q (x,y)
Hence $
  {m_1} = 2,{m_2} = 1 \\
  {x_1} = 2,{x_2} = - 2 \\
  {y_1} = - 7,{y_2} = 4 \\
$
$x = \dfrac{{{m_1}{x_2} + {m_2}{x_1}}}{{{m_1} + {m_2}}} = \dfrac{{2 \times \left( { - 7} \right) + 1 \times 2}}{{1 + 2}} = \dfrac{{ - 14 + 2}}{3} = - 4$
$y = \dfrac{{{m_1}{y_2} + {m_2}{y_1}}}{{{m_1} + {m_2}}} = \dfrac{{2 \times 4 + 1 \times \left( { - 2} \right)}}{{1 + 2}} = 2$
Hence, point Q ( -4, 2 ).

Note: Whenever we get this type of question the key concept of solving is first we Have to draw a diagram according to question and then we have to trisect a line that means divide in three equal parts but we can say as divide in the ratio 1:2 as drawn in diagram to solve easily.