Question

Find the coordinates of the incentre of the triangle, equations of whose sides are
$x + 1 = 0, - 3x + 4y + 5 = 0,5x + 12y = 27$

Answer 1

Hint: Take the given three equations, and the point of intersections and the co-ordinates. Once you find the coordinates find the length of the sides of the triangle with the help of the distance formula and then at last use the formula of incentre and place the values and simplify.

Complete step-by-step answer:
By solving the given equations and find the bisectors.
Let us consider lines
 $
  l:x + 1 = 0, \\
  m: - 3x + 4y + 5 = 0, \\
  n:5x + 12y = 27 \\
 $

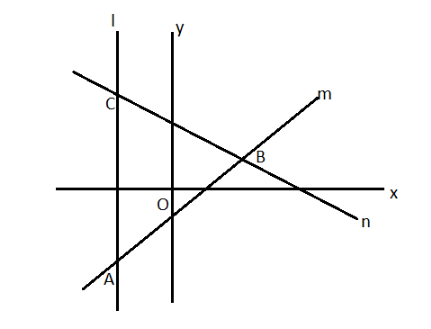
Now, using the equation of line “l” and “m” find the coordinates-
$
  x + 1 = 0 \\
   \Rightarrow x = ( - 1) \\
 $
Place the value of “x” in the equation of line “m”
$
   - 3x + 4y + 5 = 0 \\
   \Rightarrow - 3( - 1) + 4y + 5 = 0 \;
 $
Simplify the above equation –
$
   \Rightarrow 3 + 4y + 5 = 0 \\
   \Rightarrow 8 + 4y = 0 \\
 $
Make “y” the subject –
$
   \Rightarrow 4y = - 8 \\
   \Rightarrow y = \dfrac{{ - 8}}{4} \\
   \Rightarrow y = ( - 2) \\
 $
Therefore, the coordinates of the vertices as $A( - 1, - 2)$
Similarly finding the coordinates for the lines “m” and “n”
$
- 3x + 4y + 5 = 0{\text{ }}...{\text{ (a)}} \\
  5x + 12y = 27{\text{ }}...{\text{ (b)}} \\
 $
Make the coefficient of the equations (a) and (b) common. So, multiply equation (a) with $5$ and multiply equation (b) with$3$.
$
   \Rightarrow - 15x + 20y + 25 = 0{\text{ }}...{\text{ (c)}} \\
   \Rightarrow 15x + 36y = 81{\text{ }}...{\text{ (d)}} \\
 $
Add equations (c) and (d)
$ \Rightarrow 56y + 25 = 81$
Simplification –
$
   \Rightarrow 56y = 81 - 25 \\
   \Rightarrow 56y = 56 \\
   \Rightarrow y = 1 \;
 $
Place value of “y” in the equation “a”
$
   - 3x + 4y + 5 = 0 \\
   - 3x + 4(1) + 5 = 0 \\
   - 3x + 9 = 0 \;
 $
Simplify and make the subject “x”
$ \Rightarrow - 3x = - 9$
Negative sign on both the sides of the equation cancel each other –
$
   \Rightarrow 3x = 9 \\
   \Rightarrow x = \dfrac{9}{3} \\
   \Rightarrow x = 3 \;
 $
Therefore, the coordinates of the vertices as $B(3,1)$
Similarly find the point of coordinates for the lines “l” and “n”
$
  l:x + 1 = 0 \\
  n:5x + 12y = 27 \\
 $
Place $x = ( - 1)$ in the line “n”
$
   \Rightarrow 5( - 1) + 12y = 27 \\
   \Rightarrow - 5 + 12y = 27 \\
 $
Simplify and make the subject “Y”
$
   \Rightarrow 12y = 27 + 5 \\
   \Rightarrow 12y = 32 \\
   \Rightarrow y = \dfrac{{32}}{{12}} \\
   \Rightarrow y = \dfrac{8}{3} \\
 $
Therefore, the coordinates of the vertices as $C( - 1,\dfrac{8}{3})$
Now, the incentre of the triangle is
Incentre $ = \left( {\dfrac{{a{x_1} + b{x_2} + c{x_3}}}{{a + b + c}},\dfrac{{a{y_1} + b{y_2} + c{y_3}}}{{a + b + c}}} \right)$ ....... (i)
Where “a” is the measure of side “BC”
“b” is the measure of side “AC”
 “c” is the measure of side “BC”
With the help of the values of the coordinates and the distance formula-
Where
$A( - 1, - 2)$
$B(3,1)$
$C( - 1,\dfrac{8}{3})$
Now, $a = \sqrt {{{(3 + 1)}^2} + {{(1 - \dfrac{8}{3})}^2}} $
Simplification –
$
   \Rightarrow a = \sqrt {{4^2} + {{\left( {\dfrac{{ - 5}}{3}} \right)}^2}} \\
   \Rightarrow a = \sqrt {16 + \dfrac{{25}}{9}} \\
 $
Take LCM and simplify –
$
   \Rightarrow a = \sqrt {\dfrac{{144 + 25}}{9}} \\
   \Rightarrow a = \sqrt {\dfrac{{169}}{9}} \\
   \Rightarrow a = \dfrac{{13}}{3} \\
 $
Now, similarly $b = \dfrac{{14}}{3}$
And $c = 5$
Now, place the value in the equation (i)
Incentre $ = \left( {\dfrac{{a{x_1} + b{x_2} + c{x_3}}}{{a + b + c}},\dfrac{{a{y_1} + b{y_2} + c{y_3}}}{{a + b + c}}} \right)$
Incentre $ = \left( {\dfrac{{\dfrac{{13}}{3}( - 1) + \dfrac{{14}}{3}(3) + 5( - 1)}}{{\dfrac{{13}}{3} + \dfrac{{14}}{3} + 5}},\dfrac{{\dfrac{{13}}{3}( - 2) + \dfrac{{14}}{3}(1) + 5(\dfrac{8}{3})}}{{\dfrac{{13}}{3} + \dfrac{{14}}{3} + 5}},} \right)$
Take LCM and Simplify the numerator and the denominator-
Incentre $ = \left( {\dfrac{{\dfrac{{14}}{3}}}{{\dfrac{{42}}{3}}},\dfrac{{\dfrac{{28}}{3}}}{{\dfrac{{42}}{3}}}} \right)$
Numerator and the denominator being the same get canceled from both the coordinates.
Incentre $ = \left( {\dfrac{{14}}{{42}},\dfrac{{28}}{{42}}} \right)$
Common factors cancel each other from the numerator and the denominator-
Incentre $ = \left( {\dfrac{1}{3},\dfrac{2}{3}} \right)$

So, the correct answer is “Option C”.

Note: Follow all the steps carefully and wisely. It is lengthy but easy. Do not make silly mistakes while simplifying. Also, know the difference between the incircle and the centroid of the triangle and apply accordingly.