Question

Find the coordinates of focus, equation of directrix, length of latus rectum and coordinates of end point of latus rectum for the parabola ${{y}^{2}}=20x$.

Answer 1

Hint: Write the given equation of the parabola as ${{y}^{2}}=4ax$ and compare the value of ‘a’. Now, the directrix of this parabola will be x = -a, coordinates of focus will be S(a, 0), length of latus rectum will be 4a and the coordinates of its end point will be lying on the parabola with x coordinates as a. Substitute this value in the parabola to get the y coordinates of the end point.

Complete step-by-step solution:
Here we have been provided with the equation of a parabola as ${{y}^{2}}=20x$ and we are asked to find its coordinates of focus, equation of directrix, length of latus rectum and coordinates of end point of latus rectum.
Now, we know that general equation of a parabola whose lies on the origin is given as ${{y}^{2}}=4ax$ where the directrix of this parabola is x = -a, coordinates of focus is S(a, 0), length of latus rectum is 4a and the coordinates of its end point is lying on the parabola with x coordinates as a. Geometrically it is shown as:

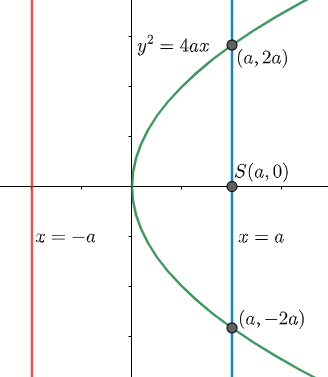
Now, we can write ${{y}^{2}}=20x$as:
$\Rightarrow {{y}^{2}}=4\times 5\times x$
On comparing it with ${{y}^{2}}=4ax$ we have a = 5. So, we have the following results about this parabola.
(1) Coordinates of focus are S(a, 0).
(2) Equation of directrix is x = -5. Directrix is the line on which if we will draw a perpendicular from any point on the parabola then its length will be equal to the distance between the point on the parabola and the focus S, i.e. its eccentricity is 1.
(3) Latus rectum is a line perpendicular to the x axis passing though the focus S(a, 0). Now, since this line passes through the focus (5, 0) so we can determine the y coordinate by substituting the value of x coordinate in the equation of the parabola ${{y}^{2}}=20x$, so we get,
$\begin{align}
  & \Rightarrow {{y}^{2}}=20\times 5 \\
 & \Rightarrow {{y}^{2}}=100 \\
\end{align}$
Taking square root both the sides we get,
$\Rightarrow y=\pm 10$
Therefore, the coordinates of the end points of the latus rectum is (5, 10) and (5, -10). So the length of the latus rectum will be given by the distance formula $l=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ where ‘l’ is the length of the latus rectum. Considering $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 5,10 \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)=\left( 5,-10 \right)$ we get,
$\begin{align}
  & \Rightarrow l=\sqrt{{{\left( 5-5 \right)}^{2}}+{{\left( -10-10 \right)}^{2}}} \\
 & \Rightarrow l=\sqrt{400} \\
 & \therefore l=20 \\
\end{align}$

Note: Note that if the parabola would have been of the type ${{x}^{2}}=4ay$ then we would have simply replaced x with y in all the expression we have found for the parabola ${{y}^{2}}=4ax$. Like the coordinates of focus will become (0, a), equation of directrix will become y = -a and so on. The difference between the graph of the two parabolas is that ${{y}^{2}}=4ax$ opens leftward or rightward according to the negative or positive value of ‘a’ respectively and ${{x}^{2}}=4ay$ opens upward or downward depending on the positive or negative value of ‘a’ respectively.