Question

Find the complete solution set for the inequation $\sqrt{18+x} < 2-x$?
(a) $\left[ -18,-2 \right]$
(b) $\left( -\infty ,-2 \right)\cup \left( 7,\infty \right)$
(c) $\left( -18,-2 \right)\cup \left( 7,\infty \right)$
(d) $\left[ -18,-2 \right)$

Answer 1

Hint: We start solving the problem by finding the interval for all values of x at which the given inequation is defined first. We use the property that for a function $\sqrt{g\left( x \right)}$ is defined only if $g\left( x \right)\ge 0$ for the function $\sqrt{18+x}$. We then use the property $\sqrt{18+x}\ge 0$ to find the interval for the values of x at which the function $2-x$ can be defined. We then find take the inequation $\sqrt{18+x} < 2-x$ and make the necessary calculations and use the property that if the inequality is defined as $\left( x-a \right)\left( x-b \right) > 0$ and $a < b$, then the solution set of the inequality is $x < a\text{ or }x > b$ to find the required solution set.

Complete step by step answer:
According to the problem, we need to find the complete solution set of the inequation $\sqrt{18+x} < 2-x$.
Let us first find the value for which the given inequation is defined.
We know that for a function $\sqrt{g\left( x \right)}$ is defined only if $g\left( x \right)\ge 0$.
So, we have $18+x\ge 0$.
$\Rightarrow x\ge -18$.
$\Rightarrow x\in \left[ -18,\infty \right)$ ---(1).
We know that the $2-x$ is a polynomial and we can see that all of its values should be greater than zero as we know that the value of the $\sqrt{18+x}\ge 0$.
So, we have $2-x > 0$.
$\Rightarrow x < 2$.
$\Rightarrow x\in \left( -\infty ,2 \right)$ ---(2).
The common interval of x for which the given inequation is defined will be the intersection of the values of x obtained in equations (1) and (2).
So, the inequation $\sqrt{18+x} < 2-x$ is defined on $x\in \left[ -18,2 \right)$ ---(3).
Now, let us find the solution set for the inequation $\sqrt{18+x} < 2-x$.
\[\Rightarrow {{\left( \sqrt{18+x} \right)}^{2}}<{{\left( 2-x \right)}^{2}}\].
\[\Rightarrow 18+x<4-4x+{{x}^{2}}\].
\[\Rightarrow {{x}^{2}}-5x-14 > 0\].
\[\Rightarrow {{x}^{2}}-7x+2x-14 > 0\].
\[\Rightarrow x\left( x-7 \right)+2\left( x-7 \right) > 0\].
\[\Rightarrow \left( x+2 \right)\left( x-7 \right) > 0\].
\[\Rightarrow \left( x-\left( -2 \right) \right)\left( x-7 \right) > 0\] ---(4).
We know that if the inequality is defined as $\left( x-a \right)\left( x-b \right) > 0$ and $a < b$, then the solution set of the inequality is $x < a\text{ or }x > b$. Using this we get the solution set for inequality in equation (4) as $x < -2\text{ or }x > 7$.
From equation (3), we remove the values of x which were not satisfying the interval $x < -2\text{ or }x > 7$ to get the complete solution set.
So, we get the solution set for the inequality as $x\in \left[ -18,-2 \right)$.

So, the correct answer is “Option d”.

Note: We should not consider negative square roots while finding the solution set of the given inequalities as it will not always be true which we can see in this problem. We can also solve this problem by drawing the plots of $\sqrt{x+18}$ and $2-x$ as shown below.

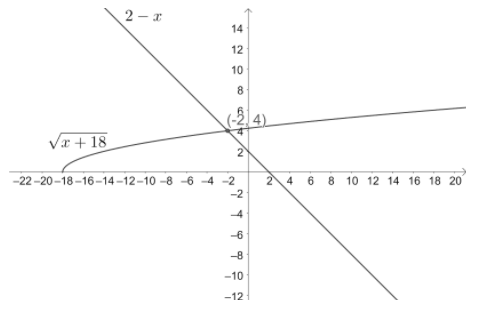
From this plot we can see that the values of $\sqrt{x+18}$ lies below the line $2-x$ in the interval $\left[ -18,-2 \right)$.