Question

Find the common tangents of the circles \[{x^2} + {y^2} = 1\] and\[{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 4\].

Answer 1

Hint: First of all, find the centre and radius of the given circles and find the internal and external centre of similitudes. Then find the pair of transverse common tangents and direct common tangents to the given circles. S, use this concept to reach the solution.
Complete step-by-step answer:
Given circle equations are \[{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 4\] and \[{x^2} + {y^2} = 1\]
We know that for the circle equation \[{\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {a^2}\] the centre of the circle is \[\left( {h,k} \right)\] and radius of the circle is \[a\].
So, for the circle equation \[{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 4\] the centre is \[{C_1}\left( {1,3} \right)\] and radius is \[{r_1} = 2\].
We know that for the circle equation \[{x^2} + {y^2} = {a^2}\] the centre of the circle is \[\left( {0,0} \right)\] and radius of the circle is \[a\].
So, for the circle equation \[{x^2} + {y^2} = 1\] the centre is \[{C_2}\left( {0,0} \right)\] and radius is \[{r_2} = 1\].
We know that the distance between the points \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\] is given by \[\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \].
Now, consider the distance between the centres of the two circles i.e.,
\[{C_1}{C_2} = \sqrt {{{\left( {1 - 0} \right)}^2} + {{\left( {3 - 0} \right)}^2}} = \sqrt {10} \]
As \[{C_1}{C_2} > {r_1} + {r_2} \Rightarrow \sqrt {10} > 2 + 1\], there will be four common tangents to the circles as shown in the below figure:

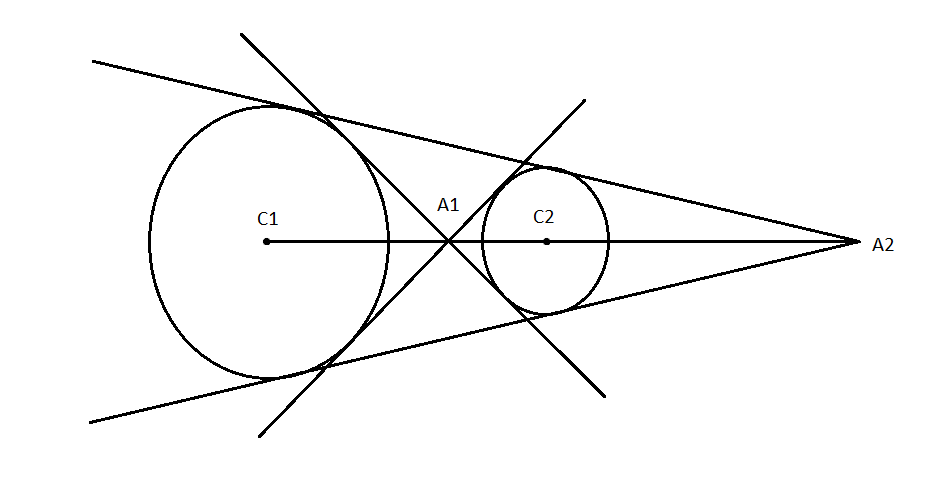
We know that if a point \[C\] divides the two points \[A\left( {{x_1},{y_1}} \right)\] and \[B\left( {{x_2},{y_2}} \right)\] in the ratio \[p:q\] the point \[C\] is given by \[C = \left( {\dfrac{{p{x_2} + q{x_1}}}{{p + q}},\dfrac{{p{y_2} + q{y_1}}}{{p + q}}} \right)\].
So, the internal centre of similitude, \[{A_1}\] divides \[{C_1}{C_2}\] in the ratio \[2:1\] internally is given by
\[
   \Rightarrow {A_1} = \left( {\dfrac{{2\left( 1 \right) + 1\left( 0 \right)}}{{2 + 1}},\dfrac{{2\left( 3 \right) + 1\left( 0 \right)}}{{2 + 1}}} \right) \\
  \therefore {A_1} = \left( {\dfrac{2}{3},\dfrac{6}{3}} \right) = \left( {\dfrac{2}{3},2} \right) \\
 \]
We know that the equation to the pair of transverse common tangents at point \[\left( {h,k} \right)\] to the circle \[{x^2} + {y^2} = {a^2}\] is given by \[{\left( {xh + yk - {a^2}} \right)^2} = \left( {{h^2} + {k^2} - {a^2}} \right)\left( {{x^2} + {y^2} - {a^2}} \right)\]
So, equation to the pair of transverse common tangents at \[\left( {\dfrac{2}{3},2} \right)\] to the circle \[{x^2} + {y^2} = 1\] is
\[
   \Rightarrow {\left( {x\left( {\dfrac{2}{3}} \right) + y\left( 2 \right) - 1} \right)^2} = \left( {{{\left( {\dfrac{2}{3}} \right)}^2} + {{\left( 2 \right)}^2} - 1} \right)\left( {{x^2} + {y^2} - 1} \right) \\
   \Rightarrow {\left( {\dfrac{{2x}}{3} + 2y - 1} \right)^2} = \left( {\dfrac{4}{9} + 4 - 1} \right)\left( {{x^2} + {y^2} - 1} \right) \\
 \]
Opening the terms inside the brackets by using the formula \[{\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ca\], we have
\[
   \Rightarrow {\left( {\dfrac{{2x}}{3}} \right)^2} + \left( {2y} \right) + \left( 1 \right) + 2\left( {\dfrac{{2x}}{3}} \right)\left( {2y} \right) + 2\left( {2y} \right)\left( { - 1} \right) + 2\left( {\dfrac{{2x}}{3}} \right)\left( { - 1} \right) = \left( {\dfrac{4}{9} + 3} \right)\left( {{x^2} + {y^2} - 1} \right) \\
   \Rightarrow \dfrac{{4{x^2}}}{9} + 4{y^2} + 1 + \dfrac{{8xy}}{3} - 4y - \dfrac{{4x}}{3} = \left( {\dfrac{{4 + 27}}{9}} \right)\left( {{x^2} + {y^2} - 1} \right) \\
   \Rightarrow \dfrac{{4{x^2} + 36{y^2} + 9 + 24xy - 36y - 12x}}{9} = \left( {\dfrac{{31}}{9}} \right)\left( {{x^2} + {y^2} - 1} \right) \\
 \]
Cancelling and grouping the common terms, we have
\[
   \Rightarrow 4{x^2} + 24xy + 36{y^2} - 36y - 12x + 9 = 31{x^2} + 31{y^2} - 31 \\
   \Rightarrow 31{x^2} - 4{x^2} - 24xy + 31{y^2} - 36{y^2} + 12x + 36y - 31 - 9 = 0 \\
  \therefore 27{x^2} - 24xy - 5{y^2} + 12x + 36y - 40 = 0 \\
 \]
We know that if a point \[C\] divides the two points \[A\left( {{x_1},{y_1}} \right)\] and \[B\left( {{x_2},{y_2}} \right)\] in the ratio \[p:q\] the point \[C\] is given by \[C = \left( {\dfrac{{p{x_2} + q{x_1}}}{{p + q}},\dfrac{{p{y_2} + q{y_1}}}{{p + q}}} \right)\].
So, the external centre of similitude, \[{A_2}\] divides \[{C_1}{C_2}\] in the ratio \[2:1\] externally is given by
\[
   \Rightarrow {A_2} = \left( {\dfrac{{2\left( 1 \right) - 1\left( 0 \right)}}{{2 - 1}},\dfrac{{2\left( 3 \right) - 1\left( 0 \right)}}{{2 - 1}}} \right) \\
  \therefore {A_2} = \left( {2,6} \right) \\
 \]
We know that the equation to the pair of direct common tangents at point \[\left( {h,k} \right)\] to the circle \[{x^2} + {y^2} = {a^2}\] is given by \[{\left( {xh + yk - {a^2}} \right)^2} = \left( {{h^2} + {k^2} - {a^2}} \right)\left( {{x^2} + {y^2} - {a^2}} \right)\]
So, equation to the pair of direct common tangents at \[\left( {2,6} \right)\] to the circle \[{x^2} + {y^2} = 1\] is
\[
   \Rightarrow {\left( {x\left( 2 \right) + y\left( 6 \right) - 1} \right)^2} = \left( {{{\left( 2 \right)}^2} + {{\left( 6 \right)}^2} - 1} \right)\left( {{x^2} + {y^2} - 1} \right) \\
   \Rightarrow {\left( {2x + 6y - 1} \right)^2} = \left( {4 + 36 - 1} \right)\left( {{x^2} + {y^2} - 1} \right) \\
 \]
Opening the terms inside the brackets, we have
\[
   \Rightarrow 4{x^2} + 36{y^2} + 1 + 2\left( {2x} \right)\left( {6y} \right) + 2\left( {2x} \right)\left( { - 1} \right) + 2\left( {6y} \right)\left( { - 1} \right) = \left( {39} \right)\left( {{x^2} + {y^2} - 1} \right) \\
   \Rightarrow 4{x^2} + 36{y^2} + 1 + 24xy - 4x - 12y = 39{x^2} + 39{y^2} - 39 \\
   \Rightarrow 39{x^2} - 4{x^2} + 39{y^2} - 36{y^2} - 24xy + 4x + 12y - 39 - 1 = 0 \\
  \therefore 35{x^2} - 24xy + 3{y^2} + 4x + 12y - 40 = 0 \\
 \]
Thus, the common tangents are \[27{x^2} - 24xy - 5{y^2} + 12x + 36y - 40 = 0\] and \[35{x^2} - 24xy + 3{y^2} + 4x + 12y - 40 = 0\].
Note: The equation to the pair of transverse common tangents at point \[\left( {h,k} \right)\] to the circle \[{x^2} + {y^2} = {a^2}\] is given by \[{\left( {xh + yk - {a^2}} \right)^2} = \left( {{h^2} + {k^2} - {a^2}} \right)\left( {{x^2} + {y^2} - {a^2}} \right)\]. The equation to the pair of direct common tangents at point \[\left( {h,k} \right)\] to the circle \[{x^2} + {y^2} = {a^2}\] is given by \[{\left( {xh + yk - {a^2}} \right)^2} = \left( {{h^2} + {k^2} - {a^2}} \right)\left( {{x^2} + {y^2} - {a^2}} \right)\].