Question

Find the common factors of \[14pq\], \[28{p^2}{q^2}\].
A.\[14pq\]
B.\[28p\]
C.\[2pq\]
D.\[p\]

Answer 1

Hint: Here, we will find the factorization of both the numbers \[14pq\] and \[28{p^2}{q^2}\] using the highest common factor, that is, H.C.F. Then we will compare the factors to find the common factors.

Complete step-by-step answer:
We are given that the \[14pq\], \[28{p^2}{q^2}\].
First, we will consider \[14pq\].
Rewrite the above expression, we get
\[
   \Rightarrow 14pq = 14 \times p \times q \\
   \Rightarrow 14pq = 2 \times 7 \times p \times q{\text{ .......eq.(1)}} \\
 \]
Now we will consider \[28{p^2}{q^2}\].
Rewrite the above expression, we get
\[
   \Rightarrow 28{p^2}{q^2} = 28 \times {p^2} \times {q^2} \\
   \Rightarrow 28{p^2}{q^2} = 28 \times p \times p \times q \times q{\text{ ......eq.(2)}} \\
 \]
Factorize 28 from the right hand side of the above equation using the H.C.F., we get

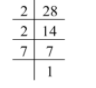
So, the factors of 28 are \[2 \times 2 \times 7\].
Using these factors in equation (2), we get
\[ \Rightarrow 28{p^2}{q^2} = 2 \times 2 \times 7 \times p \times p \times q \times q{\text{ .......eq.(3)}}\]
Finding the common factors from equation (1) and equation (3), we get
\[
   \Rightarrow {\text{Common Factors}} = 2 \times 7 \times p \times q \\
   \Rightarrow {\text{Common Factors}} = 14 \times pq \\
   \Rightarrow {\text{Common Factors}} = 14pq \\
 \]
Hence, the option A will be correct.

Note: We are supposed to write the values properly to avoid any miscalculation. The common factor is a factor of two or more numbers. When we find all the factors of two or more numbers, and some factors are the same, then the largest of those common factors in the Highest Common Factor.