
Find the coefficient of ${{x}^{4}}$ in the expansion of
${{(2-4x+3{{x}^{2}})}^{-2}}$.
Answer
597k+ views
- Hint: Assume that the roots of the quadratic expression $3{{x}^{2}}-4x+2=0$ are a and b. Hence write $\dfrac{1}{{{\left( 3{{x}^{2}}-4x+2 \right)}^{2}}}$ as $\dfrac{1}{9}{{\left( \dfrac{1}{\left( x-a \right)\left( x-b \right)} \right)}^{2}}$. Decompose $\dfrac{1}{\left( x-a \right)\left( x-b \right)}$ into partial fractions by multiplying and dividing numerator by $b-a$ and writing b-a as (x-a)-(x-b). Use the identity ${{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}$ and binomial theorem for non-integral powers and hence find the coefficient of ${{x}^{4}}$ in the expansion of the term.
Complete step-by-step solution -
Let the roots of the quadratic expression $3{{x}^{2}}-4x+2=0$ be a and b.
Hence, we have
$3{{x}^{2}}-4x+2=3\left( x-a \right)\left( x-b \right)$
Hence, the given expression(E say) becomes
$E=\dfrac{1}{9}{{\left( \dfrac{1}{\left( x-a \right)\left( x-b \right)} \right)}^{2}}$
Inside the square term multiplying numerator and denominator by a-b, we get
$E=\dfrac{1}{9{{\left( a-b \right)}^{2}}}{{\left( \dfrac{a-b}{\left( x-a \right)\left( x-b \right)} \right)}^{2}}$
Writing a-b as (x-b)-(x-a) in the numerator, we get
$E=\dfrac{1}{9{{\left( a-b \right)}^{2}}}{{\left( \dfrac{x-b-\left( x-a \right)}{\left( x-a \right)\left( x-b \right)} \right)}^{2}}$
Using $\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}$, we get
$E=\dfrac{1}{9{{\left( a-b \right)}^{2}}}{{\left( \dfrac{1}{x-a}-\dfrac{1}{x-b} \right)}^{2}}$
Using the identity ${{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}$, we get
$E=\dfrac{1}{9{{\left( a-b \right)}^{2}}}\left( \dfrac{1}{{{\left( x-a \right)}^{2}}}+\dfrac{1}{{{\left( x-b \right)}^{2}}}+\dfrac{2}{\left( x-a \right)\left( x-b \right)} \right)$
From the above procedure, we know that $\dfrac{1}{\left( x-a \right)\left( x-b \right)}=\dfrac{1}{a-b}\left( \dfrac{1}{x-a}-\dfrac{1}{x-b} \right)$
Hence, we have
$E=\dfrac{1}{9{{\left( a-b \right)}^{2}}}\left( \dfrac{1}{{{\left( x-a \right)}^{2}}}+\dfrac{1}{{{\left( x-b \right)}^{2}}}+\dfrac{2}{a-b}\left( \dfrac{1}{x-a}-\dfrac{1}{x-b} \right) \right)$
Consider the term $\dfrac{1}{{{\left( x-a \right)}^{2}}}$
We know from binomial theorem for real exponents
${{\left( 1+x \right)}^{n}}=1+nx+\dfrac{n\left( n-1 \right)}{2!}{{x}^{2}}+\cdots $
Hence, we have
${{\left( x-a \right)}^{-2}}={{a}^{-2}}{{\left( 1-\dfrac{x}{a} \right)}^{-2}}=\dfrac{1}{{{a}^{2}}}\left( 1+\dfrac{2x}{a}+\dfrac{3!}{2!}{{\left( \dfrac{x}{a} \right)}^{2}}+\dfrac{4!}{3!}{{\left( \dfrac{x}{a} \right)}^{3}}+\dfrac{5!}{4!}{{\left( \dfrac{x}{a} \right)}^{4}}+O\left( {{x}^{5}} \right) \right)$
Hence the coefficient of ${{x}^{4}}$ in the expansion of $\dfrac{1}{{{\left( x-a \right)}^{2}}}$ is $\dfrac{5}{{{a}^{6}}}$
Similarly, the coefficient of ${{x}^{4}}$ in the expansion of $\dfrac{1}{{{\left( x-b \right)}^{2}}}$ is $\dfrac{5}{{{b}^{6}}}$
Consider the term $\dfrac{1}{x-a}$
We know from binomial theorem for real exponents
${{\left( 1+x \right)}^{n}}=1+nx+\dfrac{n\left( n-1 \right)}{2!}{{x}^{2}}+\cdots $
Hence, we have
${{\left( x-a \right)}^{-1}}=-{{a}^{-1}}{{\left( 1-\dfrac{x}{a} \right)}^{-1}}=-\dfrac{1}{a}\left( 1+\dfrac{x}{a}+{{\left( \dfrac{x}{a} \right)}^{2}}+{{\left( \dfrac{x}{a} \right)}^{3}}+{{\left( \dfrac{x}{a} \right)}^{4}}+O\left( {{x}^{5}} \right) \right)$
Hence the coefficient of ${{x}^{4}}$ in the expansion of $\dfrac{1}{\left( x-a \right)}$ is $-\dfrac{1}{{{a}^{5}}}$
Similarly, the coefficient of ${{x}^{4}}$ in the expansion of $\dfrac{1}{x-b}$ is $-\dfrac{1}{{{b}^{5}}}$
Hence, the coefficient of ${{x}^{4}}$ in the expansion of E is $\dfrac{1}{9{{\left( a-b \right)}^{2}}}\left( \dfrac{5}{{{a}^{6}}}+\dfrac{5}{{{b}^{6}}}-\dfrac{2}{a-b}\left( -\dfrac{1}{{{a}^{5}}}+\dfrac{1}{{{b}^{5}}} \right) \right)=\dfrac{1}{9{{\left( a-b \right)}^{2}}}\left( \dfrac{5}{{{\left( ab \right)}^{6}}}\left( {{a}^{6}}+{{b}^{6}} \right)-\dfrac{2\left( {{a}^{5}}-{{b}^{5}} \right)}{\left( a-b \right){{\left( ab \right)}^{5}}} \right)$
Dividing ${{a}^{5}}-{{b}^{5}}$ by a-b
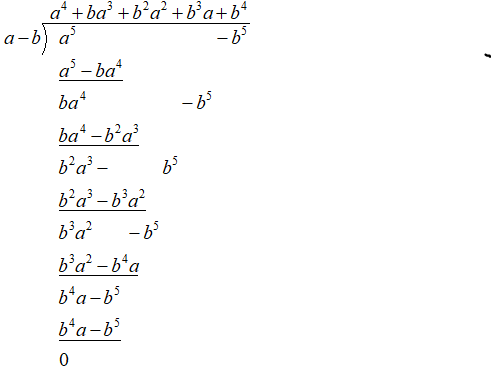
Hence, we have $\dfrac{{{a}^{5}}-{{b}^{5}}}{a-b}=\left( {{a}^{4}}+{{b}^{4}}+ab\left( {{a}^{2}}+{{b}^{2}} \right)+{{a}^{2}}{{b}^{2}} \right)$
Hence, the coefficient of ${{x}^{4}}$ in the expansion of E is
$\dfrac{1}{9{{\left( a-b \right)}^{2}}}\left( \dfrac{5}{{{\left( ab \right)}^{6}}}\left( {{a}^{6}}+{{b}^{6}} \right)-\dfrac{2\left( {{a}^{4}}+{{b}^{4}}+ab\left( {{a}^{2}}+{{b}^{2}} \right)+{{a}^{2}}{{b}^{2}} \right)}{{{\left( ab \right)}^{5}}} \right)$
Now, we have $a+b=\dfrac{4}{3},ab=\dfrac{2}{3}$
Hence, we have
${{\left( a-b \right)}^{2}}={{\left( a+b \right)}^{2}}-4ab=\dfrac{16}{9}-\dfrac{8}{3}=\dfrac{-8}{9}$
Also, we have
$\begin{align}
& {{a}^{2}}+{{b}^{2}}={{\left( a+b \right)}^{2}}-2ab=\dfrac{16}{9}-\dfrac{4}{3}=\dfrac{4}{9} \\
& {{a}^{4}}+{{b}^{4}}={{\left( {{a}^{2}}+{{b}^{2}} \right)}^{2}}-2{{\left( ab \right)}^{2}}=\dfrac{16}{81}-2\times \dfrac{4}{9}=\dfrac{16}{81}-\dfrac{8}{9}=\dfrac{-56}{81} \\
& {{a}^{6}}+{{b}^{6}}=\left( {{a}^{2}}+{{b}^{2}} \right)\left( {{a}^{4}}+{{b}^{4}}-{{\left( ab \right)}^{2}} \right)=\dfrac{4}{9}\left( \dfrac{-56}{81}-\dfrac{4}{9} \right)=\dfrac{-368}{729} \\
\end{align}$
Hence, we have
The coefficient of ${{x}^{4}}$ in the expansion of E is
$\dfrac{1}{9\left( \dfrac{-8}{9} \right)}\left( \dfrac{5}{{{\left( \dfrac{2}{3} \right)}^{6}}}\left( \dfrac{-368}{729} \right)+\dfrac{2}{{{\left( \dfrac{2}{3} \right)}^{5}}}\left( \dfrac{-56}{81}+\dfrac{2}{3}\left( \dfrac{4}{9} \right)+{{\left( \dfrac{2}{3} \right)}^{2}} \right) \right)=\dfrac{59}{16}$
Hence the coefficient of ${{x}^{4}}$ in the expansion of ${{(2-4x+3{{x}^{2}})}^{-2}}$ is $\dfrac{59}{16}$
Note: These types of questions usually involve long and cumbersome calculations, and hence a student is likely to make calculation mistakes. So we should try to minimise calculations as much as possible. In the above question, we minimise our calculation by converting to partial fractions and finding the coefficients of individual terms in summation rather than in product which made the calculations relatively easy.
Complete step-by-step solution -
Let the roots of the quadratic expression $3{{x}^{2}}-4x+2=0$ be a and b.
Hence, we have
$3{{x}^{2}}-4x+2=3\left( x-a \right)\left( x-b \right)$
Hence, the given expression(E say) becomes
$E=\dfrac{1}{9}{{\left( \dfrac{1}{\left( x-a \right)\left( x-b \right)} \right)}^{2}}$
Inside the square term multiplying numerator and denominator by a-b, we get
$E=\dfrac{1}{9{{\left( a-b \right)}^{2}}}{{\left( \dfrac{a-b}{\left( x-a \right)\left( x-b \right)} \right)}^{2}}$
Writing a-b as (x-b)-(x-a) in the numerator, we get
$E=\dfrac{1}{9{{\left( a-b \right)}^{2}}}{{\left( \dfrac{x-b-\left( x-a \right)}{\left( x-a \right)\left( x-b \right)} \right)}^{2}}$
Using $\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}$, we get
$E=\dfrac{1}{9{{\left( a-b \right)}^{2}}}{{\left( \dfrac{1}{x-a}-\dfrac{1}{x-b} \right)}^{2}}$
Using the identity ${{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}$, we get
$E=\dfrac{1}{9{{\left( a-b \right)}^{2}}}\left( \dfrac{1}{{{\left( x-a \right)}^{2}}}+\dfrac{1}{{{\left( x-b \right)}^{2}}}+\dfrac{2}{\left( x-a \right)\left( x-b \right)} \right)$
From the above procedure, we know that $\dfrac{1}{\left( x-a \right)\left( x-b \right)}=\dfrac{1}{a-b}\left( \dfrac{1}{x-a}-\dfrac{1}{x-b} \right)$
Hence, we have
$E=\dfrac{1}{9{{\left( a-b \right)}^{2}}}\left( \dfrac{1}{{{\left( x-a \right)}^{2}}}+\dfrac{1}{{{\left( x-b \right)}^{2}}}+\dfrac{2}{a-b}\left( \dfrac{1}{x-a}-\dfrac{1}{x-b} \right) \right)$
Consider the term $\dfrac{1}{{{\left( x-a \right)}^{2}}}$
We know from binomial theorem for real exponents
${{\left( 1+x \right)}^{n}}=1+nx+\dfrac{n\left( n-1 \right)}{2!}{{x}^{2}}+\cdots $
Hence, we have
${{\left( x-a \right)}^{-2}}={{a}^{-2}}{{\left( 1-\dfrac{x}{a} \right)}^{-2}}=\dfrac{1}{{{a}^{2}}}\left( 1+\dfrac{2x}{a}+\dfrac{3!}{2!}{{\left( \dfrac{x}{a} \right)}^{2}}+\dfrac{4!}{3!}{{\left( \dfrac{x}{a} \right)}^{3}}+\dfrac{5!}{4!}{{\left( \dfrac{x}{a} \right)}^{4}}+O\left( {{x}^{5}} \right) \right)$
Hence the coefficient of ${{x}^{4}}$ in the expansion of $\dfrac{1}{{{\left( x-a \right)}^{2}}}$ is $\dfrac{5}{{{a}^{6}}}$
Similarly, the coefficient of ${{x}^{4}}$ in the expansion of $\dfrac{1}{{{\left( x-b \right)}^{2}}}$ is $\dfrac{5}{{{b}^{6}}}$
Consider the term $\dfrac{1}{x-a}$
We know from binomial theorem for real exponents
${{\left( 1+x \right)}^{n}}=1+nx+\dfrac{n\left( n-1 \right)}{2!}{{x}^{2}}+\cdots $
Hence, we have
${{\left( x-a \right)}^{-1}}=-{{a}^{-1}}{{\left( 1-\dfrac{x}{a} \right)}^{-1}}=-\dfrac{1}{a}\left( 1+\dfrac{x}{a}+{{\left( \dfrac{x}{a} \right)}^{2}}+{{\left( \dfrac{x}{a} \right)}^{3}}+{{\left( \dfrac{x}{a} \right)}^{4}}+O\left( {{x}^{5}} \right) \right)$
Hence the coefficient of ${{x}^{4}}$ in the expansion of $\dfrac{1}{\left( x-a \right)}$ is $-\dfrac{1}{{{a}^{5}}}$
Similarly, the coefficient of ${{x}^{4}}$ in the expansion of $\dfrac{1}{x-b}$ is $-\dfrac{1}{{{b}^{5}}}$
Hence, the coefficient of ${{x}^{4}}$ in the expansion of E is $\dfrac{1}{9{{\left( a-b \right)}^{2}}}\left( \dfrac{5}{{{a}^{6}}}+\dfrac{5}{{{b}^{6}}}-\dfrac{2}{a-b}\left( -\dfrac{1}{{{a}^{5}}}+\dfrac{1}{{{b}^{5}}} \right) \right)=\dfrac{1}{9{{\left( a-b \right)}^{2}}}\left( \dfrac{5}{{{\left( ab \right)}^{6}}}\left( {{a}^{6}}+{{b}^{6}} \right)-\dfrac{2\left( {{a}^{5}}-{{b}^{5}} \right)}{\left( a-b \right){{\left( ab \right)}^{5}}} \right)$
Dividing ${{a}^{5}}-{{b}^{5}}$ by a-b
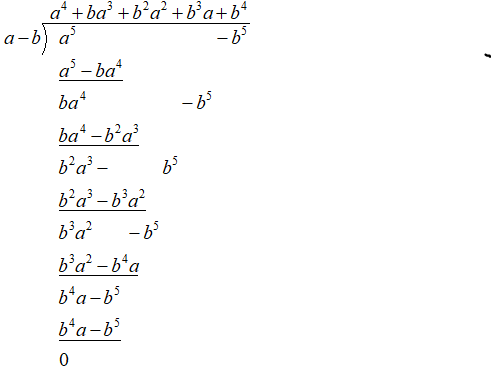
Hence, we have $\dfrac{{{a}^{5}}-{{b}^{5}}}{a-b}=\left( {{a}^{4}}+{{b}^{4}}+ab\left( {{a}^{2}}+{{b}^{2}} \right)+{{a}^{2}}{{b}^{2}} \right)$
Hence, the coefficient of ${{x}^{4}}$ in the expansion of E is
$\dfrac{1}{9{{\left( a-b \right)}^{2}}}\left( \dfrac{5}{{{\left( ab \right)}^{6}}}\left( {{a}^{6}}+{{b}^{6}} \right)-\dfrac{2\left( {{a}^{4}}+{{b}^{4}}+ab\left( {{a}^{2}}+{{b}^{2}} \right)+{{a}^{2}}{{b}^{2}} \right)}{{{\left( ab \right)}^{5}}} \right)$
Now, we have $a+b=\dfrac{4}{3},ab=\dfrac{2}{3}$
Hence, we have
${{\left( a-b \right)}^{2}}={{\left( a+b \right)}^{2}}-4ab=\dfrac{16}{9}-\dfrac{8}{3}=\dfrac{-8}{9}$
Also, we have
$\begin{align}
& {{a}^{2}}+{{b}^{2}}={{\left( a+b \right)}^{2}}-2ab=\dfrac{16}{9}-\dfrac{4}{3}=\dfrac{4}{9} \\
& {{a}^{4}}+{{b}^{4}}={{\left( {{a}^{2}}+{{b}^{2}} \right)}^{2}}-2{{\left( ab \right)}^{2}}=\dfrac{16}{81}-2\times \dfrac{4}{9}=\dfrac{16}{81}-\dfrac{8}{9}=\dfrac{-56}{81} \\
& {{a}^{6}}+{{b}^{6}}=\left( {{a}^{2}}+{{b}^{2}} \right)\left( {{a}^{4}}+{{b}^{4}}-{{\left( ab \right)}^{2}} \right)=\dfrac{4}{9}\left( \dfrac{-56}{81}-\dfrac{4}{9} \right)=\dfrac{-368}{729} \\
\end{align}$
Hence, we have
The coefficient of ${{x}^{4}}$ in the expansion of E is
$\dfrac{1}{9\left( \dfrac{-8}{9} \right)}\left( \dfrac{5}{{{\left( \dfrac{2}{3} \right)}^{6}}}\left( \dfrac{-368}{729} \right)+\dfrac{2}{{{\left( \dfrac{2}{3} \right)}^{5}}}\left( \dfrac{-56}{81}+\dfrac{2}{3}\left( \dfrac{4}{9} \right)+{{\left( \dfrac{2}{3} \right)}^{2}} \right) \right)=\dfrac{59}{16}$
Hence the coefficient of ${{x}^{4}}$ in the expansion of ${{(2-4x+3{{x}^{2}})}^{-2}}$ is $\dfrac{59}{16}$
Note: These types of questions usually involve long and cumbersome calculations, and hence a student is likely to make calculation mistakes. So we should try to minimise calculations as much as possible. In the above question, we minimise our calculation by converting to partial fractions and finding the coefficients of individual terms in summation rather than in product which made the calculations relatively easy.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




