Question

How do you find the circumference and area of a circle that has a rectangle inscribed inside it with sides that are 9 by 12?

Answer 1

Hint: We know that if a circle inscribed right angle at circumference on then the angle is subtended by diameter. Now we will find the length of the diameter by using Pythagoras theorem. Now we know that the area of the circle is given by $\pi {{r}^{2}}$ and circumference of the circle is given by $2\pi r$ where r is the radius of the circle.

Complete step-by-step answer:
Now first let us draw the figure with given conditions.

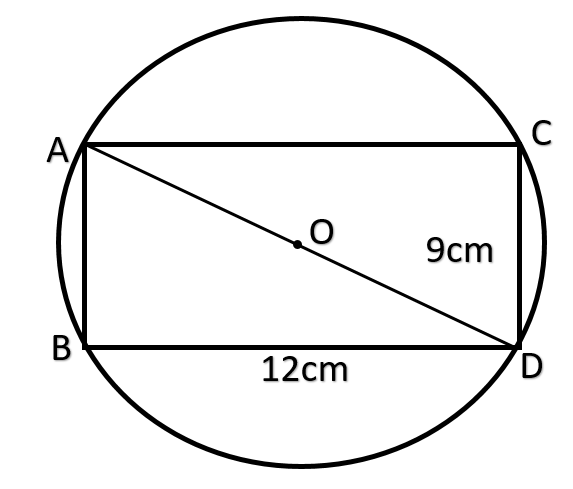
Now we know that ABCD is a rectangle and hence, BD = AC = 12cm and CD = AB = 9cm.
Now we have a property of a circle which says if the angles made on circumference is ${{90}^{\circ }}$ then the angle is always subtended by diameter.
Now we know that all the angles of the rectangle are ${{90}^{\circ }}$. Hence we can say that AD is the diameter of the circle.
Now note by using Pythagoras theorem we have $A{{B}^{2}}+B{{C}^{2}}=A{{D}^{2}}$
Hence substituting the values we get,
$\begin{align}
  & \Rightarrow {{9}^{2}}+{{12}^{2}}=A{{D}^{2}} \\
 & \Rightarrow 81+144=A{{D}^{2}} \\
 & \Rightarrow 225=A{{D}^{2}} \\
 & \Rightarrow AD=15 \\
\end{align}$
Hence we have AD = 15cm.
Hence the diameter of the circle is 15cm
Now we know that the circumference of the circle is given by $2\pi r=\pi d$ where r is the radius of the circle and d is the diameter of the circle.
Hence we have the circumference of the circle is $15\pi cm$ .
Also we know that the area of the circle is given by $\pi {{r}^{2}}=\pi {{\left( \dfrac{d}{2} \right)}^{2}}$
Hence we have area of the given circle is $\pi {{\left( \dfrac{15}{2} \right)}^{2}}=\dfrac{225\pi }{4}c{{m}^{2}}$
Hence we have the circumference and area of the circles are $15\pi $ and $\left( \dfrac{225\pi }{4} \right)c{{m}^{2}}$

Note: Now we have that an angle subtended by an arc at centre is double the angle subtended by the angle on any point on circumference of the circle. Hence we have that the angle which makes the right angle on circumference will subtend an angle of ${{180}^{\circ }}$ at centre and hence the angle is nothing but diameter of the circle.