Question

Find the circumcenter of the triangle formed by the lines $x + y + 2 = 0$, $5x - y - 2 = 0$ and $x - 2y + 5 = 0$.

Answer 1

Hint: Solve the given equations pairwise to obtain the vertices of the triangle. Substitute the coordinates of the vertices in the general equation of a circle ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$ with $\left( {h,k} \right)$ as its center. Solve the equations thus obtained to get $\left( {h,k} \right)$ which is the required answer.

Complete step by step answer:
We are given the equation of the lines which form the sides of the triangle.
$ \Rightarrow $ Line 1: $x + y + 2 = 0$
$ \Rightarrow $ Line 2: $5x - y - 2 = 0$
$ \Rightarrow $ Line 3: $x - 2y + 5 = 0$
We need to find the circumcenter of the triangle.

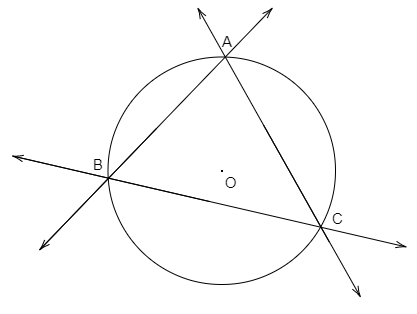
In the above figure, consider O as the circumcenter of $\Delta ABC$.
Consider the system of linear equations,
Transform line 1 in slope-intercept form,
$ \Rightarrow y = - x - 2$ ….. (1)
Transform line 2 in slope-intercept form,
$ \Rightarrow y = 5x - 2$ ….. (2)
Transform line 3 in slope-intercept form,
$ \Rightarrow y = \dfrac{1}{2}\left( {x + 5} \right)$ ….. (3)
As can be understood from the figure, every pair of lines has a point of intersection, and these 3 points of intersection form the vertices of the triangle.
Equate equation (1) and (2),
$ \Rightarrow - x - 2 = 5x - 2$
Move the variable part on one side and constant part on another side,
$ \Rightarrow 5x + x = 2 - 2$
Simplify the term,
$ \Rightarrow 6x = 0$
Divide both sides by 6,
$ \Rightarrow x = 0$
Substitute the value in equation (1),
$ \Rightarrow y = - 0 - 2$
Simplify the terms,
$ \Rightarrow y = - 2$
Thus, we get one of the vertices of the triangle. Call this vertex as A.
$A \equiv \left( {0, - 2} \right)$
Now, equate equation (2) and (3),
$ \Rightarrow 5x - 2 = \dfrac{1}{2}\left( {x + 5} \right)$
Cross multiply the terms,
$ \Rightarrow 10x - 4 = x + 5$
Move the variable part on one side and constant part on another side,
$ \Rightarrow 10x - x = 5 + 4$
Simplify the term,
$ \Rightarrow 9x = 9$
Divide both sides by 9,
$ \Rightarrow x = 1$
Substitute the value in equation (2),
$ \Rightarrow y = 5 \times 1 - 2$
Simplify the terms,
$ \Rightarrow y = 3$
Thus, we get the second vertices of the triangle. Call this vertex as B.
$B \equiv \left( {1,3} \right)$
Now, equate equation (1) and (3),
$ \Rightarrow - x - 2 = \dfrac{1}{2}\left( {x + 5} \right)$
Cross multiply the terms,
$ \Rightarrow - 2x - 4 = x + 5$
Move the variable part on one side and constant part on another side,
$ \Rightarrow - 2x - x = 5 + 4$
Simplify the term,
$ \Rightarrow - 3x = 9$
Divide both sides by -3,
$ \Rightarrow x = - 3$
Substitute the value in equation (1),
$ \Rightarrow y = - \left( { - 3} \right) - 2$
Simplify the terms,
$ \Rightarrow y = 1$
Thus, we get the third vertices of the triangle. Call this vertex as C.
$B \equiv \left( { - 3,1} \right)$
Now, these vertices of $\Delta ABC$ lie on the circle and we need only 3 points to construct a circle.
The center of the circle formed by the vertices A, B, C is the required circumcenter.
We will construct the equation of the circle using A, B, and C.
Let $\left( {h,k} \right)$ be the circumcenter.
Then the equation of the circle with radius r and center $\left( {h,k} \right)$ is given by,
${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$
As the points A, B, and C lie on the circle, they will satisfy the above equation.
For point A,
$ \Rightarrow {\left( {0 - h} \right)^2} + {\left( { - 2 - k} \right)^2} = {r^2}$ ….. (4)
For point B,
$ \Rightarrow {\left( {1 - h} \right)^2} + {\left( {3 - k} \right)^2} = {r^2}$ ….. (5)
For point C,
$ \Rightarrow {\left( { - 3 - h} \right)^2} + {\left( {1 - k} \right)^2} = {r^2}$ ….. (6)
Comparing the equations (4) and (5), we get,
$ \Rightarrow {\left( {0 - h} \right)^2} + {\left( { - 2 - k} \right)^2} = {\left( {1 - h} \right)^2} + {\left( {3 - k} \right)^2}$
Expand the terms,
$ \Rightarrow {h^2} + 4 + {k^2} + 4k = 1 + {h^2} + 2h + 9 + {k^2} - 6k$
Simplify the terms,
$ \Rightarrow 2h - 10k = - 6$ ….. (7)
Comparing the equations (4) and (6), we get,
$ \Rightarrow {\left( {0 - h} \right)^2} + {\left( { - 2 - k} \right)^2} = {\left( { - 3 - h} \right)^2} + {\left( {1 - k} \right)^2}$
Expand the terms,
$ \Rightarrow {h^2} + 4 + {k^2} + 4k = 9 + {h^2} + 6h + 1 + {k^2} - 2k$
Simplify the terms,
$ \Rightarrow 6h - 6k = - 6$
Divide both sides by 6,
$ \Rightarrow h - k = - 1$
Move k on the right side,
$ \Rightarrow h = k - 1$ ….. (8)
Substitute the value in equation (7),
$ \Rightarrow 2\left( {k - 1} \right) - 10k = - 6$
Expand the bracket,
$ \Rightarrow 2k - 2 - 10k = - 6$
Simplify the term,
$ \Rightarrow - 8k = - 4$
Divide both sides by -8,
$ \Rightarrow k = \dfrac{1}{2}$
Substitute the value in equation (8),
$ \Rightarrow h = \dfrac{1}{2} - 1$
Simplify the terms,
$ \Rightarrow h = - \dfrac{1}{2}$
So, $\left( {h,k} \right) \equiv \left( { - \dfrac{1}{2},\dfrac{1}{2}} \right)$

Hence, the circumcenter is $\left( { - \dfrac{1}{2},\dfrac{1}{2}} \right)$.

Note: In the given $\Delta ABC$, the line passing through the circumcenter and the vertex A is the perpendicular bisector of its opposite side BC. This holds for all the vertices.
The circumcenter of a triangle is defined as the point of intersection of the perpendicular bisectors of the sides of the triangle.