Question

Find the centroid of a triangle whose vertices are \[\left( {3,4} \right),\left( { - 7, - 2} \right){\text{ and }}\left( {10, - 5} \right)\].

Answer 1

Hint:Median is a line that joins the midpoint of a side and the opposite vertex of the triangle. The point of intersection of all the three medians of a triangle is called a centroid. It is denoted by \[G\]. From the question we have all the three vertices of the triangle. So, we will use the formula for calculating the centroid of a triangle.

Formula used:
Centroid of a triangle with vertices \[\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right){\text{ and }}\left( {{x_3},{y_3}} \right)\] is;
\[G = \left[ {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right]\]

Complete step by step answer:

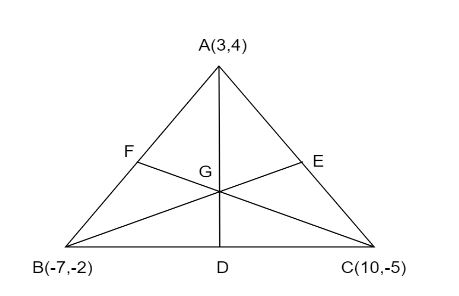
Let \[ABC\] be a triangle with the vertices given in the questions.Let \[AD,BE,CF\] are the medians on the triangle \[ABC\]. We can see from the figure that the medians intersect at point \[G\]. So, \[G\] is the centroid of the triangle \[ABC\].Now we will find the coordinates of \[G\] using the formula.We have;
\[G = \left[ {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right]\]
Now we will put the value of \[{x_1},{x_2},{x_3}\] and \[{y_1},{y_2},{y_3}\] from the coordinates of the given vertices. So, we get;
\[ \Rightarrow G = \left[ {\dfrac{{3 - 7 + 10}}{3},\dfrac{{4 - 2 - 5}}{3}} \right]\]
On solving we get;
\[ \Rightarrow G = \left[ {\dfrac{6}{3},\dfrac{{ - 3}}{3}} \right]\]
On dividing we get;
\[ \Rightarrow G = \left[ {2, - 1} \right]\]

Hence the centroid of the triangle is \[\left( {2, - 1} \right)\].

Note:One thing to note here is that the centroid of a triangle cannot lie outside of the triangle. It always lies inside the triangle. Also, in an equilateral triangle the centroid, the circumcentre, the incentre and the orthocentre coincides.The centroid theorem states that the centroid of a triangle is at \[\dfrac{2}{3}\] of the distance from the vertex to the midpoint of the sides. In a square, the point of intersection of the diagonals is the centroid of the square.