Question

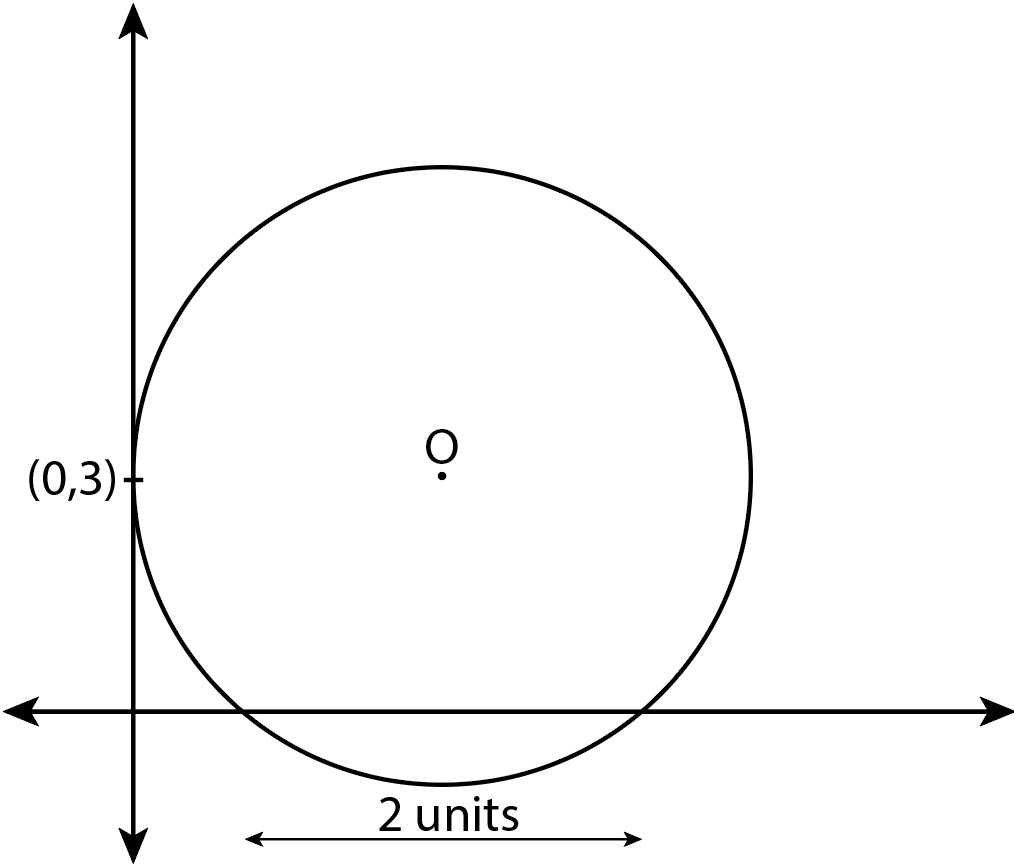
Find the centre of the circle touching Y-axis at (0,3) and making an intercept 2 units on positive X-axis is
A. $\left( {\sqrt {10} ,3} \right)$
B. $\left( {3,\sqrt {10} } \right)$
C. $\left( { - \sqrt {10} ,3} \right)$
D. $\left( { - \sqrt {10} , - 3} \right)$

Answer 1

Hint: Let the equation of circle be ${x^2} + {y^2} + 2gx + 2fy + c = 0$ .
Using the information provided in question find the value of f.
Now that we have the value of g, we can find the value of g using the formula \[2\sqrt {{g^2} - {f^2}} = 2\] .
Thus, we get the centre of the circle as (g,f).

Complete step-by-step answer:
It is given that a circle is touching the Y-axis at (0,3) and making an intercept 2 units on the positive X-axis.

Let the equation of the circle be ${x^2} + {y^2} + 2gx + 2fy + c = 0$ ... (1)
The circle touches Y-axis, so, $c = {f^2}$ ... (2)
Substituting equation (2) in equation (1) gives
 ${x^2} + {y^2} + 2gx + 2fy + {f^2} = 0$ ... (3)
As given, the circle touches the Y-axis at (0,3).
So, the point (0,3) must lie on the circle i.e. it must satisfy the equation of circle (equation (3)).
 $\Rightarrow $ Substituting the values x = 0 and y = 3, in equation (3)
 $\Rightarrow {\left( 0 \right)^2} + {\left( 3 \right)^2} + 2g\left( 0 \right) + 2f\left( 3 \right) + {f^2} = 0$
 $\therefore 9 + 6f + {f^2} = 0$
 $
  \Rightarrow {f^2} + 2\left( 3 \right)\left( f \right) + 9 = 0 \\
  \Rightarrow {\left( {f + 3} \right)^2} = 0 \\
  \Rightarrow f + 3 = 0 \\
  \Rightarrow f = - 3 \\
 $
It is also given that, circle makes an intercept of 2 on the positive X-axis.
So, \[2\sqrt {{g^2} - {f^2}} = 2\]
 $
  \Rightarrow \sqrt {{g^2} - {f^2}} = 1 \\
  \Rightarrow \sqrt {{g^2} - {{\left( { - 3} \right)}^2}} = 1 \\
  \therefore \sqrt {{g^2} - 9} = 1 \\
 $
Now, squaring both sides
 $
  \Rightarrow {g^2} - 9 = 1 \\
  \Rightarrow {g^2} = 1 + 9 \\
  \Rightarrow {g^2} = 10 \\
  \Rightarrow g = \sqrt {10} \\
 $
Thus, we get the centre of the circle as $\left( {\sqrt {10} ,3} \right)$ .
Option (A) is correct.
Note: It is given that a circle is touching Y-axis at (0,3) and making an intercept 2 units on the positive X-axis.
     

Thus, from the above diagram it is clear that, the coordinates of O will be O(x,3) as the perpendicular drawn from O to X-axis will be of length 3 units and radius of circle will be its x coordinate.
               

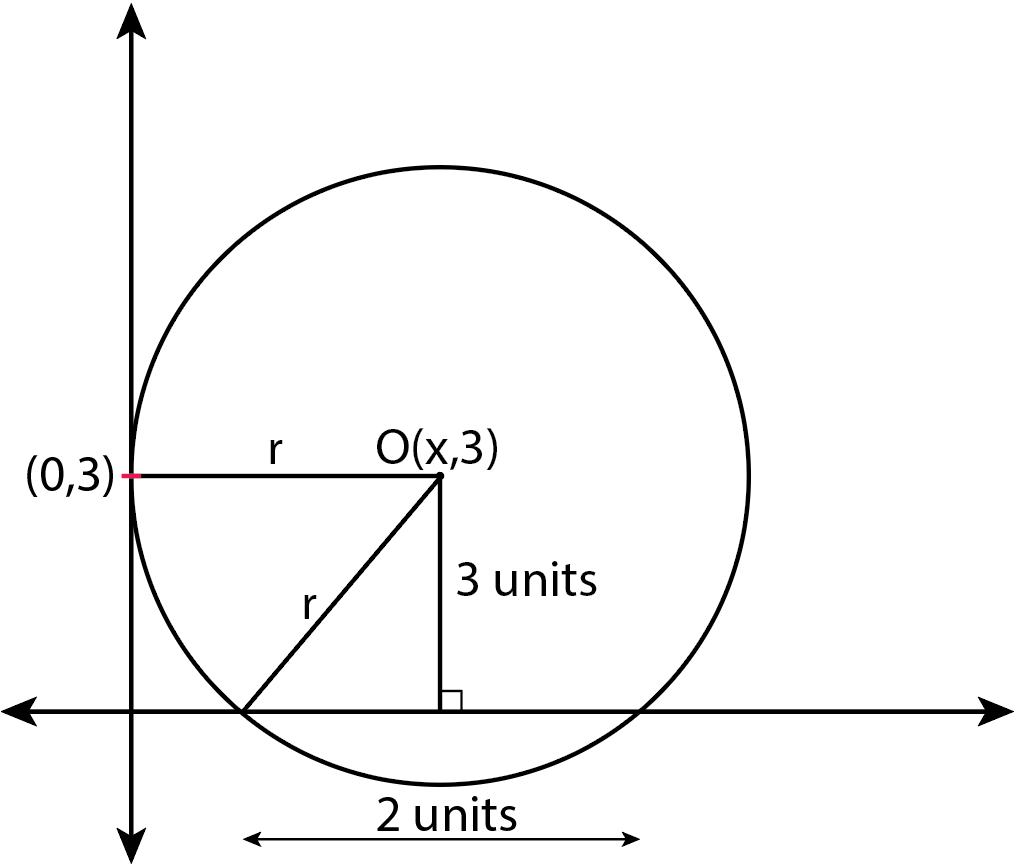
Also, the perpendicular from O to X-axis, bisects the 2 unit intercept. Let M be the point on X-axis be the foot of perpendicular from O. So, coordinates of M(1,0).
     

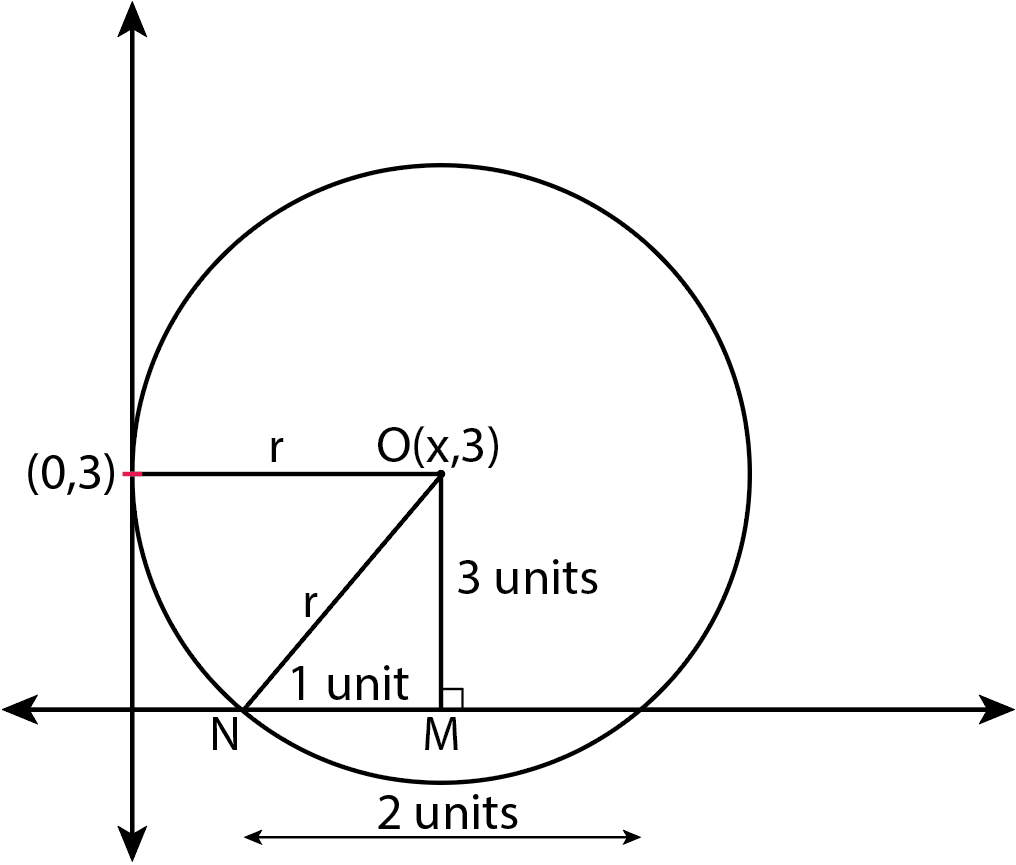
Also, OMN is a right angled triangle. So, applying Pythagoras’ theorem to it will give radius r.
 \[\Rightarrow r = \sqrt {{3^2} + {1^2}} \]
        \[
   = \sqrt {9 + 1} \\
   = \sqrt {10} \\
 \]
Thus, we get the coordinates of O as $\left( {\sqrt {10} ,3} \right)$ . Here, x coordinate of O is equal to r.
So, the centre of the circle is $\left( {\sqrt {10} ,3} \right)$ .