Question

Find the center of mass of a uniform semi-circular ring of radius R.

Answer 1

Hint: The center of mass of a regular uniform object can be found by finding the center of mass of a point infinitesimal mass and integrating this for the whole object. This can be done by finding out a relation between the mass and another variable in the body with respect to which the relation can be integrated for the whole body to get the center of mass of the whole body.

Formula used:
The center of mass $\left( {{C}_{x}},{{C}_{y}} \right)$ with respect to a reference point $\left( x,y \right)$ is given by
$\left( {{C}_{x}},{{C}_{y}} \right)=\left( \dfrac{\sum{M{{r}_{x}}}}{\sum{M}},\dfrac{\sum{M{{r}_{y}}}}{\sum{M}} \right)$
where ${{r}_{x}}$ and ${{r}_{y}}$ are the horizontal and vertical positions of the mass $M$with respect to the point $\left( x,y \right)$.

Complete step-by-step answer:
Let us first draw a diagram for the ring along with proper coordinates.

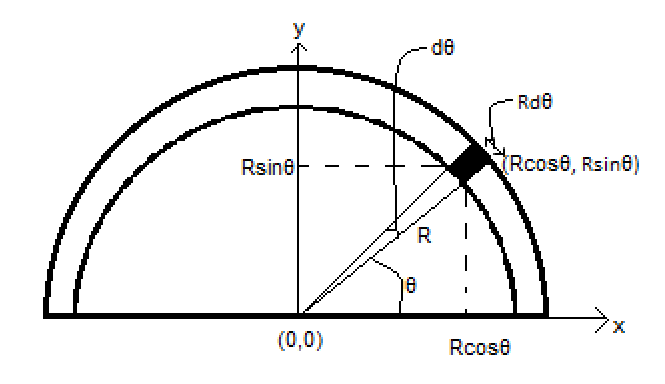
We will take the origin and the axes as shown in the figure.
Since the ring is uniform, it has a constant mass per unit length $\left( \lambda \right)$.
Let the total mass of the Ring be $M$ and its total circumference is $\pi R$. Therefore, by definition,
$\lambda =\dfrac{M}{\pi R}$ --(1)
We will take an infinitesimal strip of mass $dM$as shown in the figure. The coordinates of the strip are as shown, that is, $\left( R\cos \theta ,R\sin \theta \right)$. The length of the strip is as shown, that is, $Rd\theta $, where $d\theta $is an infinitesimal angle and $\theta $ is the angle made by the line joining the strip to the origin with the x-axis.
Therefore, using the definition of $\lambda $, we get, $dM=\lambda Rd\theta $ --(2)
Now, the center of mass $\left( {{C}_{x}},{{C}_{y}} \right)$ with respect to a reference point $\left( x,y \right)$ is given by $\left( {{C}_{x}},{{C}_{y}} \right)=\left( \dfrac{\sum{M{{r}_{x}}}}{\sum{M}},\dfrac{\sum{M{{r}_{y}}}}{\sum{M}} \right)$ --(3) where ${{r}_{x}}$ and ${{r}_{y}}$ are the horizontal and vertical positions of the mass $M$with respect to the point $\left( x,y \right)$.
We will take the reference point as the origin $\left( 0,0 \right)$.
Hence, we will find the center of mass by using (3) and integrating the small strip to cover the whole length of the ring. The mass of the strip is $dm$ and its positions with respect to the origin are $\left( R\cos \theta ,R\sin \theta \right)$.
Therefore, using (3)
${{C}_{x}}=\dfrac{\int\limits_{0}^{M}{R\cos \theta dm}}{\int\limits_{0}^{M}{dM}}$ $\therefore {{C}_{x}}=\dfrac{\int\limits_{0}^{\pi }{R\cos \theta \lambda Rd\theta }}{\int\limits_{0}^{M}{dM}}$ --[using (2)]
$\therefore {{C}_{x}}=\dfrac{\int\limits_{0}^{\pi }{\lambda {{R}^{2}}\cos \theta d\theta }}{\int\limits_{0}^{M}{dM}}=\dfrac{\lambda {{R}^{2}}\int\limits_{0}^{\pi }{\cos \theta d\theta }}{\int\limits_{0}^{M}{dM}}=\dfrac{\lambda {{R}^{2}}\left[ \sin \theta \right]_{0}^{\pi }}{\left[ M \right]_{0}^{M}}=\dfrac{\lambda {{R}^{2}}\left[ \sin \pi -\sin 0 \right]}{M-0}=\dfrac{\lambda {{R}^{2}}\left[ 0-0 \right]}{M}=0$
Similarly,
${{C}_{y}}=\dfrac{\int\limits_{0}^{M}{R\sin \theta dm}}{\int\limits_{0}^{M}{dM}}$ $\therefore {{C}_{y}}=\dfrac{\int\limits_{0}^{\pi }{R\sin \theta \lambda Rd\theta }}{\int\limits_{0}^{M}{dM}}$ --[using (2)]
    $\therefore {{C}_{y}}=\dfrac{\int\limits_{0}^{\pi }{\lambda {{R}^{2}}\sin \theta d\theta }}{\int\limits_{0}^{M}{dM}}=\dfrac{\lambda {{R}^{2}}\int\limits_{0}^{\pi }{\sin \theta d\theta }}{\int\limits_{0}^{M}{dM}}=\dfrac{\lambda {{R}^{2}}\left[ -\cos \theta \right]_{0}^{\pi }}{\left[ M \right]_{0}^{M}}=\dfrac{-\lambda {{R}^{2}}\left[ \left( -1 \right)-1 \right]}{M-0}=\dfrac{\lambda {{R}^{2}}\left[ 2 \right]}{M}=\dfrac{2\lambda {{R}^{2}}}{M}$
$\therefore {{C}_{y}}=\dfrac{2\dfrac{M}{\pi R}{{R}^{2}}}{M}=\dfrac{2R}{\pi }$
Hence, $\left( {{C}_{x}},{{C}_{y}} \right)=\left( 0,\dfrac{2R}{\pi } \right)$.
Hence, the center of mass of a semi circular ring lies on the vertical passing through its center of curvature at a distance of $\dfrac{2R}{\pi }$from the center of curvature.

Note: It can also be noted that since the semi circular ring is symmetric about the vertical y-axis, the abscissa of the center of mass lies on the vertical axis itself. Thus, there was no need to find ${{C}_{x}}$and we could have said that it would be zero by stating the reason for symmetry of the body. However, it is still a good practice to prove the same mathematically. However, in situations where saving time is a priority, such as in competitive exams, such conclusions based on symmetry of the body should be considered by the student.