Question

How will you find the center and vertices of the hyperbola mentioned in the equation \[4{{y}^{2}}-9{{x}^{2}}=36\], also sketch the hyperbola.

Answer 1

Hint: From the question that has been mentioned above we will first be changing the equation into the general equation of hyperbola then we will equate it with the general equation and find the endpoints of the hyperbola i.e. a and b value from the equation. After finding a and b values we will find the vertices of the hyperbola with the formula.

Complete step-by-step solution:
So the general equation of hyperbola is
\[{{\dfrac{\left( y-k \right)}{{{a}^{2}}}}^{2}}-{{\dfrac{\left( x-h \right)}{{{b}^{2}}}}^{2}}=1\]
Where (h,k) is the center of the hyperbola.
Now the equation that has been stated to us is \[4{{y}^{2}}-9{{x}^{2}}=36\]
We will now divide both the right hand side and the left hand side by 36 to make the right hand side value equal to one and we will get
\[\begin{align}
  & {{\dfrac{4\left( y-0 \right)}{36}}^{2}}-{{\dfrac{9\left( x-0 \right)}{36}}^{2}}=1 \\
 & \Rightarrow {{\dfrac{\left( y-0 \right)}{9}}^{2}}-{{\dfrac{\left( x-0 \right)}{4}}^{2}}=1 \\
\end{align}\]
This can also be written as
\[\Rightarrow {{\dfrac{\left( y-0 \right)}{{{3}^{2}}}}^{2}}-{{\dfrac{\left( x-0 \right)}{{{2}^{2}}}}^{2}}=1\]
Now when we equate the whole thing with the general equation of hyperbola which is \[{{\dfrac{\left( y-k \right)}{{{a}^{2}}}}^{2}}-{{\dfrac{\left( x-h \right)}{{{b}^{2}}}}^{2}}=1\], we can clearly say that the value of (h,k) is (0,0) which will then become the center of hyperbola.
Now to calculate the vertices of the hyperbola we will find the value of \[\left( h,k+a \right)\] and \[\left( h,k-a \right)\]
To calculate the above mentioned value we will use the values that we found earlier while equating the given equation with the general equation, from this we got the value of h as 0, value of k as 0, value of a as 3 and value of b as 2. So from all the values of h,k,a,b we can easily find the value of vertices that are:
\[\left( h,k+a \right)\text{ }=\text{ }\left( 0,0+3 \right)\], from this we got our first vertices i.e. (0,3)
Similarly we will calculate for \[\left( h,k-a \right)\] from this we got our second vertices as (0,-3).
So our center point came as (0,0) and vertices of the hyperbola came as (0,3) and (0,-3).
To sketch the graph of hyperbola we will use the values of a and b if the value of a is greater than b then vertices will be on the y axis and vice versa. For this equation hyperbola will come as:

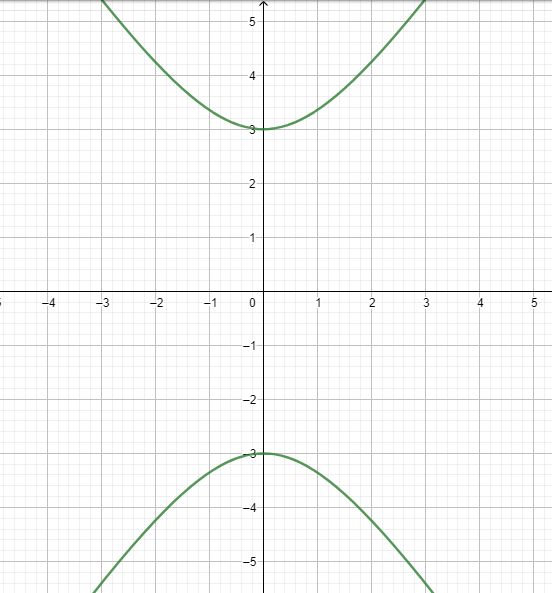
Note: The common mistakes that happen in the question is while writing the general equation we forget to mention the Y-k and x-h where h and k are the center, to not make this mistake always write the general equation beforehand to make sure you use the correct formula.