Question

How do you find the center and radius of the circle with the given equation ${x^2} + {y^2} + 4x - 8y - 44 = 0$ ?

Answer 1

Hint: There are two ways to find the radius and center of this equation. One way is the standard formula which we can apply on the equation to find the center and radius and the other one is to make the identity of algebra in x and y by adding and subtracting constants. So Here we use the algebraic identities to convert the given equation into standard form of the equation of circle and then compare it with standard form and find the radius and center.

Complete step-by-step solution:
In this question, we are given an equation of a circle whose radius and center we have to find.
We have, ${x^2} + {y^2} + 4x - 8y - 44 = 0$
Now,
We will apply the formula ${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$ or ${\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab$ to make the equation of whole square in terms of x and y.
Now,
$ \Rightarrow {x^2} + {y^2} + 4x - 8y - 44 = 0$
We can also write it as,
$ \Rightarrow {x^2} + {y^2} + 2\left( 2 \right)x - 2\left( 4 \right)y - 44 = 0$
Add and subtract ${\left( 2 \right)^2}$ in LHS,
$ \Rightarrow {x^2} + 4x + {\left( 2 \right)^2} + {y^2} - 8y - {\left( 2 \right)^2} - 44 = 0$
Now, add and subtract ${\left( 4 \right)^2}$ in LHS
$ \Rightarrow {x^2} + 4x + {\left( 2 \right)^2} + {y^2} - 8y + {\left( 4 \right)^2} - {\left( 4 \right)^2} - {\left( 2 \right)^2} - 44 = 0$
Now use ${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$ and ${\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab$
$ \Rightarrow {\left( {x + 2} \right)^2} + {\left( {y - 4} \right)^2} - 16 - 4 - 44 = 0$
On calculation, we get
$ \Rightarrow {\left( {x + 2} \right)^2} + {\left( {y - 4} \right)^2} - 64 = 0$
$ \Rightarrow {\left( {x + 2} \right)^2} + {\left( {y - 4} \right)^2} = 64$
As we know that ${\left( 8 \right)^2}\, = \,64$
$ \Rightarrow {\left( {x + 2} \right)^2} + {\left( {y - 4} \right)^2} = {\left( 8 \right)^2}$
Now, we can compare this equation with the standard equation of circle i.e. ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {\left( r \right)^2}$, where a and b are the x and y coordinates of center and r is the radius.
Now, on comparing $a\, = \, - 2\,,\,b\, = \,4,\,\,r = \,8$. Thus we get the circle as:

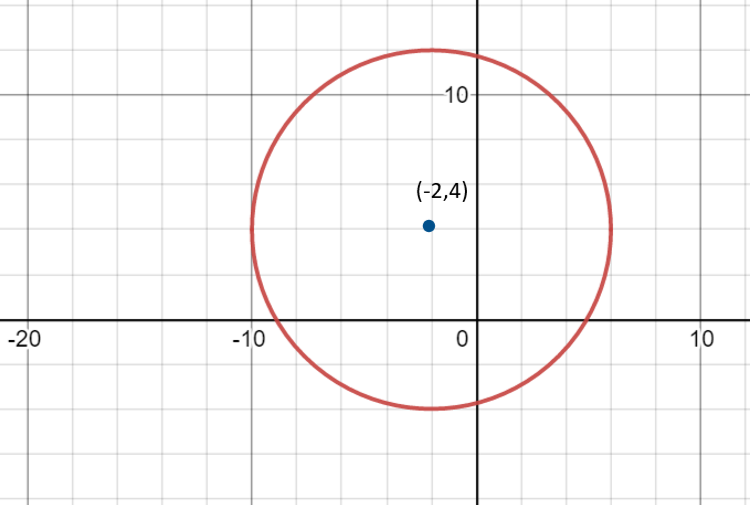
Therefore, $\left( { - 2\,,\,4} \right)$ is the center of the circle and $8$ is the radius of the circle.

Note: This is the one more method to solve this question. To get the x coordinate of the center of the circle, we divide the coefficient of x by $-2$ from the equation and similarly to get the y coordinate of the center of the circle we divide the coefficient of y by $ - 2$.
We can find the radius of circle using formula $\text{radius} = \,\sqrt {{g^2} + {f^2} - c} $ where $\left( { - g\,,\, - f} \right)$ is the center of the circle and c is the constant.