Question

How do you find the center and radius for ${{x}^{2}}+{{y}^{2}}=13$?

Answer 1

Hint: In this problem we need to find the center and radius of the given equation. We know that the standard from of the circle which is having center at $\left( a,b \right)$ and radius $r$ is given by ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$. So, we will convert the given equation in the form of the standard equation of the circle. Now we will compare both the equations to get the required values.

Complete step by step answer:
Given the equation, ${{x}^{2}}+{{y}^{2}}=13$.
Simplifying the above equation, then we will get
${{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}=13$
Comparing the above equation with the standard equation of the circle ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$. Then we will get
$a=0$, $b=0$, ${{r}^{2}}=13\Rightarrow r=\sqrt{13}$
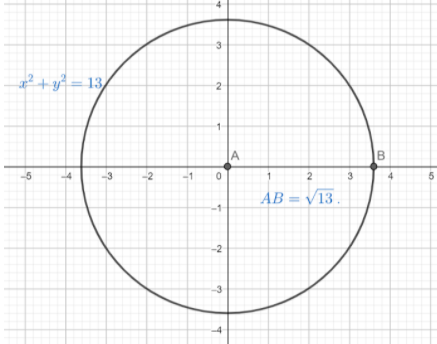
Hence the center of the circle ${{x}^{2}}+{{y}^{2}}=13$ is $\left( a,b \right)=\left( 0,0 \right)$ and the radius of the circle is $r=\sqrt{13}$. The graph of the given circle will be

Note: In this problem we have only the terms ${{x}^{2}}$, ${{y}^{2}}$ without coefficients in the given equation. So, we have easily simplified the equation and converted it into the standard form of the equation. But some time there may be coefficients for the terms ${{x}^{2}}$, ${{y}^{2}}$ and there may be terms of $x$ and $y$, then we need to rearrange the terms in the given equation and we will observe terms in the obtained equation, so that we can split the constant in the given equation and able to convert the given equation in standard form. Here we will use the algebraic formulas either ${{\left( p+q \right)}^{2}}={{p}^{2}}+{{q}^{2}}+2pq$ or ${{\left( p-q \right)}^{2}}={{p}^{2}}+{{q}^{2}}-2pq$ to simplify the equation. After converting the given equation in standard form we will compare the both the equations to get the result.