Question

How do you find the center and radius for $5{{x}^{2}}+5{{y}^{2}}+10x-30y+49=0$?

Answer 1

Hint: Divide the given equation by ‘5’ to reduce the coefficient of ‘${{x}^{2}}$’ and ‘${{y}^{2}}$’. Then convert it to the standard form of circle i.e. ${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{\left( r \right)}^{2}}$ by completing square method. Compare the modified equation to the standard form of circle to get the center and the radius.

Complete step by step solution:
The equation of circle of the form ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ can be converted to the standard form of circle i.e. ${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{\left( r \right)}^{2}}$ by completing square method. For that we have to convert the whole equation to three square terms, one of ‘x’, one of ‘y’ and one of constant.
The expression we have $5{{x}^{2}}+5{{y}^{2}}+10x-30y+49=0$
First we have to reduce the coefficient of ‘x’ and ‘y’.
So, dividing by ‘5’ throughout the equation, we get
$\begin{align}
  & \Rightarrow \dfrac{5{{x}^{2}}+5{{y}^{2}}+10x-30y+49}{5}=\dfrac{0}{5} \\
 & \Rightarrow {{x}^{2}}+{{y}^{2}}+2x-6y+\dfrac{49}{5}=0 \\
 & \Rightarrow {{\left( x \right)}^{2}}+2\cdot x\cdot 1+{{\left( 1 \right)}^{2}}-{{\left( 1 \right)}^{2}}+{{\left( y \right)}^{2}}-2\cdot y\cdot 3+{{\left( 3 \right)}^{2}}-{{\left( 3 \right)}^{2}}+\dfrac{49}{5}=0 \\
 & \Rightarrow {{\left( x+1 \right)}^{2}}+{{\left( y-3 \right)}^{2}}-1-9+\dfrac{49}{5}=0 \\
 & \Rightarrow {{\left( x+1 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=10-\dfrac{49}{5} \\
 & \Rightarrow {{\left( x+1 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=\dfrac{50-49}{5} \\
 & \Rightarrow {{\left( x+1 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=\dfrac{1}{5} \\
 & \Rightarrow {{\left( x-\left( -1 \right) \right)}^{2}}+{{\left( y-3 \right)}^{2}}={{\left( \dfrac{1}{\sqrt{5}} \right)}^{2}} \\
\end{align}$
Now it is in the required form.
Comparing the above equation with the general equation of circle, we get
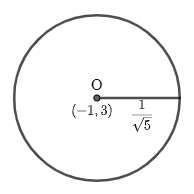
h=$-1$, k=3 and r=$\dfrac{1}{\sqrt{5}}$
Hence, the center of the given circle is ($-1$, 3) and radius is $\dfrac{1}{\sqrt{5}}$.

This is the required solution of the given question.

Note: The coefficient of ‘${{x}^{2}}$’ and ‘${{y}^{2}}$’ should be 1. So dividing the whole equation by ‘5’ should be the first approach for solving this question. In the general equation of circle ${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{\left( r \right)}^{2}}$ ‘h’ is the ‘x’- offset from the origin and ‘y’ is the ‘y’- offset from the origin.