Question

How do you find the base of a right triangle when given the hypotenuse is 14 ft. The angle formed between the hypotenuse and base is 41 degrees?

Answer 1

Hint: First assume the angle formed between the hypotenuse and base as ‘$\alpha $’. Then put the values of angle ‘$\alpha $’ and hypotenuse ‘h’ in the formula $\cos \alpha =\dfrac{b}{h}$. Do the necessary calculation to get the value of ‘b’ which is the required solution.

Complete step by step solution:

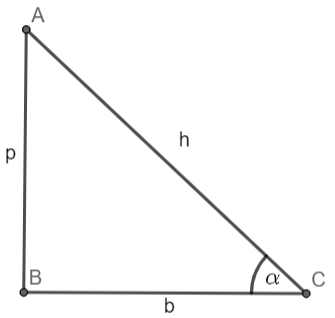
ABC is a right angle triangle with base ‘b’, perpendicular ‘p’ and hypotenuse ‘h’.
Given, the hypotenuse is 14 ft. and the angle formed between the hypotenuse and base is 41 degrees.
Let the angle formed between the hypotenuse and base is ‘$\alpha $’.
So, h=14 ft. and $\alpha ={{41}^{\circ }}$
We know, in right angle triangle ABC $\cos \alpha =\dfrac{BC}{AC}=\dfrac{b}{h}$
Putting the values of angle ‘$\alpha $’ and hypotenuse ‘h’ in $\cos \alpha =\dfrac{b}{h}$, we get
$\begin{align}
  & \Rightarrow \cos 41=\dfrac{b}{14} \\
 & \Rightarrow 0.7547\times 14=b \\
 & \Rightarrow b=10.566 \\
\end{align}$
Hence the base is 10.566 ft.
This is the required solution of the given question.

Note: Since now we have both the values of hypotenuse and base, we can also find the perpendicular using Pythagoras' theorem. For the above triangle Pythagoras' theorem can be applied as ${{h}^{2}}={{p}^{2}}+{{b}^{2}}$.
Putting the values of ‘h’ and ‘b’ in ${{h}^{2}}={{p}^{2}}+{{b}^{2}}$, we get
\[\begin{align}
  & {{14}^{2}}={{p}^{2}}+{{10.566}^{2}} \\
 & \Rightarrow 196={{p}^{2}}+111.64 \\
 & \Rightarrow 196-111.64={{p}^{2}} \\
 & \Rightarrow p=\sqrt{84.36} \\
 & \Rightarrow p=9.18 \\
\end{align}\]