Question

Find the axis of symmetry of \[f\left( x \right) = 2{x^2} - 5x + 9\].
A \[x = - \dfrac{5}{4}\]
B \[x = \dfrac{5}{4}\]
C \[x = - \dfrac{5}{2}\]
D \[x = \dfrac{5}{2}\]

Answer 1

Hint: To find the axis of symmetry, we are given with the equation which is of the form, \[a{x^2} + bx + c\], in which we need to apply the formula to find the axis of symmetry i.e., \[x = - \dfrac{b}{{2a}}\], substituting the values of a and b we get the axis of symmetry.
Formula used:
 Equation for the axis of symmetry:\[x = - \dfrac{b}{{2a}}\]
Here, \[a\] and \[b\] are coefficients.

Complete step by step answer:
 Let us write the given data:
\[f\left( x \right) = 2{x^2} - 5x + 9\]
The given equation is of the form, \[a{x^2} + bx + c\], in which
\[a = 2\], \[b = - 5\] and \[c = 9\].
We know that, the equation for the axis of symmetry is given as:
\[x = - \dfrac{b}{{2a}}\]
Now, substitute the values in the formula we have:
\[ \Rightarrow x = - \dfrac{{ - 5}}{{2\left( 2 \right)}}\]
Hence, the axis of symmetry of the given curve is:
\[ \Rightarrow x = \dfrac{5}{{2\left( 2 \right)}}\]
\[ \Rightarrow x = \dfrac{5}{4}\]

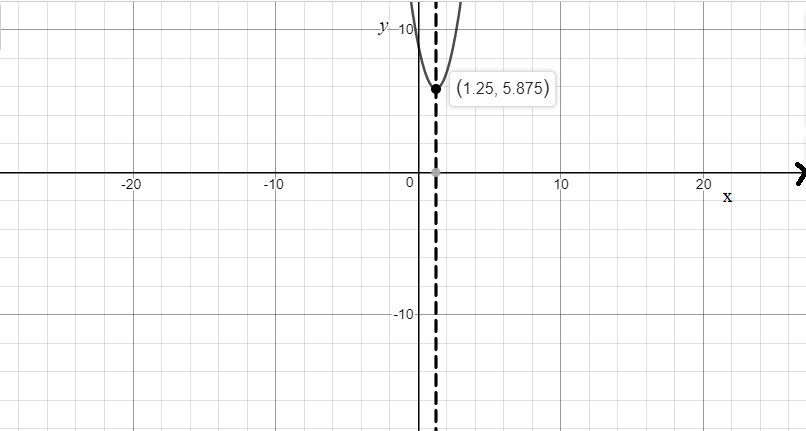
Therefore, the axis of symmetry passing through the vertex is vertical with equation \[x = \dfrac{5}{4} = 1.25\].
So, the correct answer is “Option B”.

Note: We must note that the axis of symmetry of a parabola is a line about which the parabola is symmetrical. When the parabola is vertical, the line of symmetry is vertical and when a quadratic function is graphed in the coordinate plane, the resulting parabola and corresponding axis of symmetry are vertical.