
Find the asymptotes of the curve \[y=\dfrac{3x+3}{x-3}\].
Answer
615.3k+ views
Hint:An asymptote is a line which touches the curve at infinity or we can say that it is a line such that the distance between the line and the curve approaches zero if the coordinates tend to infinity there will be two asymptotes of the given function one is horizontal and the other one is vertical. When we take denominator as equal to zero, we will get vertical asymptotes and if we take the \[\underset{x\to \infty }{\mathop{\lim }}\,\] for the function then we get horizontal asymptotes.
Complete step-by-step answer:
We have been given the curve \[y=\dfrac{3x+3}{x-3}\].
We know that there will be two asymptotes one is horizontal and the other one is vertical. By denominator is equal to zero, we get the vertical asymptotes and if we take \[x\to \infty \] limit on the function, we get horizontal asymptotes.
For the vertical asymptotes, we have,
\[\begin{align}
& x-3=0 \\
& \Rightarrow x=3 \\
\end{align}\]
Hence the vertical asymptotes is x=3.
Now for the horizontal asymptotes we have,
\[\Rightarrow Y=\underset{x\to \infty }{\mathop{\lim }}\,\left( \dfrac{3x+3}{x-3} \right)\]
On taking ‘x’ as common, we get as follows:
\[\begin{align}
& \Rightarrow Y=\underset{x\to \infty }{\mathop{\lim }}\,\dfrac{x\left( 3+\dfrac{3}{x} \right)}{x\left( 1-\dfrac{3}{x} \right)} \\
& \Rightarrow Y=\underset{x\to \infty }{\mathop{\lim }}\,\dfrac{3+\dfrac{3}{x}}{\left( 1-\dfrac{3}{x} \right)} \\
& \Rightarrow Y=3 \\
\end{align}\]
Hence the horizontal asymptote is Y=3.
Therefore, we get the asymptotes of the given function are x=3 and y=3.
Note: Sometimes we just find the vertical asymptotes and we forget about the horizontal asymptotes. So be careful while finding the horizontal asymptotes as there is a chance of calculation mistake. The graph for this question is as shown below.
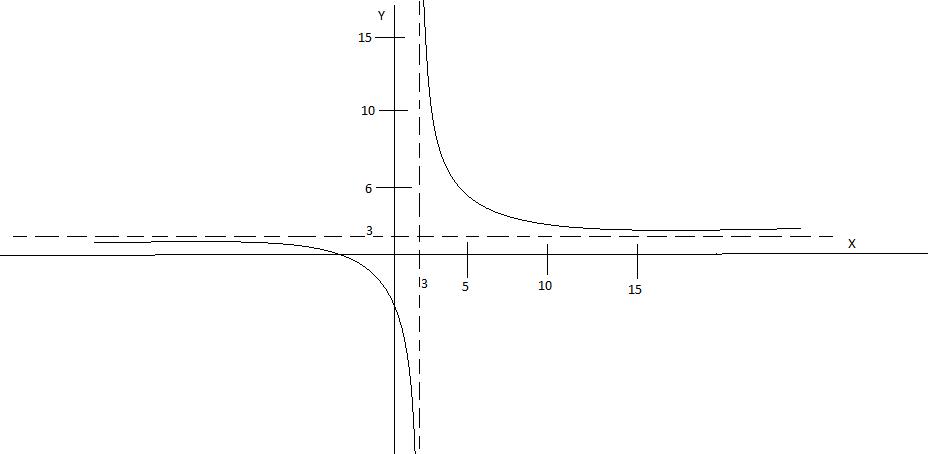
Complete step-by-step answer:
We have been given the curve \[y=\dfrac{3x+3}{x-3}\].
We know that there will be two asymptotes one is horizontal and the other one is vertical. By denominator is equal to zero, we get the vertical asymptotes and if we take \[x\to \infty \] limit on the function, we get horizontal asymptotes.
For the vertical asymptotes, we have,
\[\begin{align}
& x-3=0 \\
& \Rightarrow x=3 \\
\end{align}\]
Hence the vertical asymptotes is x=3.
Now for the horizontal asymptotes we have,
\[\Rightarrow Y=\underset{x\to \infty }{\mathop{\lim }}\,\left( \dfrac{3x+3}{x-3} \right)\]
On taking ‘x’ as common, we get as follows:
\[\begin{align}
& \Rightarrow Y=\underset{x\to \infty }{\mathop{\lim }}\,\dfrac{x\left( 3+\dfrac{3}{x} \right)}{x\left( 1-\dfrac{3}{x} \right)} \\
& \Rightarrow Y=\underset{x\to \infty }{\mathop{\lim }}\,\dfrac{3+\dfrac{3}{x}}{\left( 1-\dfrac{3}{x} \right)} \\
& \Rightarrow Y=3 \\
\end{align}\]
Hence the horizontal asymptote is Y=3.
Therefore, we get the asymptotes of the given function are x=3 and y=3.
Note: Sometimes we just find the vertical asymptotes and we forget about the horizontal asymptotes. So be careful while finding the horizontal asymptotes as there is a chance of calculation mistake. The graph for this question is as shown below.

Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Actinoid contraction is more than lanthanoid contraction class 11 chemistry CBSE

The transition element that has lowest enthalpy of class 11 chemistry CBSE

10 examples of friction in our daily life

In Dows process haloarene is converted to phenol with class 11 chemistry CBSE

During the charging of lead storage battery the reaction class 11 chemistry CBSE




