Question

How to find the asymptotes of $f\left( x \right)=\dfrac{{{x}^{2}}}{x+1}$?

Answer 1

Hint: We recall that the vertical asymptotes of the function $\dfrac{f\left( x \right)}{g\left( x \right)}=\dfrac{{{f}_{1}}\left( x \right){{f}_{2}}\left( x \right)...}{{{g}_{1}}\left( x \right){{g}_{2}}\left( x \right)...}$ are obtained as ${{g}_{i}}\left( x \right)=0,i\ge 1$ if ${{f}_{i}}\left( x \right),{{g}_{i}}\left( x \right)$ do not have common zeros for all $i\ge 1,i\in N$. The horizontals asymptotes of $\dfrac{f\left( x \right)}{g\left( x \right)}$ with the condition that degree of $f\left( x \right)$ greater than degree of $g\left( x \right)$ does not exist. We express $f\left( x \right)=\dfrac{{{x}^{2}}}{x+1}-\left( x-1 \right)=\dfrac{2}{x+1}$ to find the oblique asymptotes. \[\]

Complete step by step solution:
We know that asymptotes are lines which meet the curve of any function at infinity. We know when we are given a rational function $\dfrac{f\left( x \right)}{g\left( x \right)}$ we first factorize the numerator and denominator into linear factors as;
\[\dfrac{f\left( x \right)}{g\left( x \right)}=\dfrac{{{f}_{1}}\left( x \right){{f}_{2}}\left( x \right)...}{{{g}_{1}}\left( x \right){{g}_{2}}\left( x \right)...}\]
We find the vertical asymptotes are obtained the zeros of denominators ${{g}_{i}}\left( x \right)=0,i\ge 1$ if there are no common zeros among numerator factors and denominator factors ${{f}_{j}}\left( x \right),{{g}_{i}}\left( x \right)$ for any $i\ge 1,j\ge 1,i\in N,j\in N$. If there is a common zero say at $x=a$ which means ${{f}_{j}}\left( a \right)={{g}_{i}}\left( a \right)=0$ then we get hole in the curve of $f\left( x \right)$ at $x=a$.\[\]
We find the horizontal asymptotes comparing the degree of numerator and denominator. If the degree of numerator is $n$ and degree of denominator is $d$ and $d < n$ then there does not exist any horizontal asymptote.\[\]
We are asked to find asymptotes for
\[f\left( x \right)=\dfrac{{{x}^{2}}}{x+1}\]
We factorize the numerator and denominator to have;
\[f\left( x \right)=\dfrac{{{x}^{2}}}{x+1}=\dfrac{x\cdot x}{x+1}\]
We see that the zeros in the numerator are $x=0,0$ and in the denominator is $x=-1$. Since there are no common zeros one vertical asymptote is
\[x+1=0\Rightarrow x=-1\]
We see the degree of numerator $n=2$ and degree of denominator $d=1$. Since we have $n > d$ there will not be any horizontal asymptote. The oblique asymptotes are obtained with observation. Let us consider
\[\begin{align}
  & \dfrac{{{x}^{2}}}{x+1}=\dfrac{{{x}^{2}}-1+1}{x+1} \\
 & \Rightarrow \dfrac{{{x}^{2}}}{x+1}=\dfrac{{{x}^{2}}-1}{x+1}+\dfrac{1}{x+1} \\
 & \Rightarrow \dfrac{{{x}^{2}}}{x+1}=x-1+\dfrac{1}{x+1} \\
 & \Rightarrow \dfrac{{{x}^{2}}}{x+1}-\left( x-1 \right)=\dfrac{1}{x+1} \\
\end{align}\]
If we observe that as we increase $x$ to infinity the function $f\left( x \right)=\dfrac{{{x}^{2}}}{x+1}$ and the difference $\dfrac{1}{x+1}$ goes to zero. So $y=x-1$ is an oblique asymptote of $f\left( x \right)=\dfrac{{{x}^{2}}}{x+1}$.\[\]

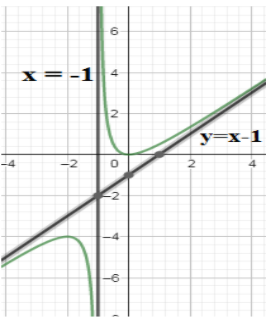
Note: We note that if $d=n$ then $y=\dfrac{a}{b}$ is a horizontal asymptote where $a,b$ are the coefficients of highest degree term in the numerator $f\left( x \right)$ and denominator $g\left( x \right)$ respectively. If $d > n$ then $y=0$ is the asymptote of $y=\dfrac{f\left( x \right)}{g\left( x \right)}$. We can also find $\displaystyle \lim_{x \to \infty }\dfrac{f\left( x \right)}{g\left( x \right)}=0$ as the horizontal asymptote.