Question

Find the area of triangle formed by the points with polar coordinates
$\left( 1,\dfrac{\pi }{6} \right),\ \left( 2,\dfrac{\pi }{3} \right),\ \left( 3,\dfrac{\pi }{2} \right)$

Answer 1

- Hint:For solving this type of sums, first of all we have to convert the polar coordinates $\left( a,\theta \right)$, into X-Y coordinates i.e. $\left( a\cos \theta ,a\sin \theta \right)$. And then find the area of triangle using the formula of determinant which is given as,
\[\Delta =\dfrac{1}{2}\left| \begin{matrix}
   {{x}_{1}} & {{y}_{1}} & 1 \\
   {{x}_{2}} & {{y}_{2}} & 1 \\
   {{x}_{3}} & {{y}_{3}} & 1 \\
\end{matrix} \right|\]

Complete step-by-step solution -

Now, as given in the question we have to find the area of polar coordinates $\left( 1,\dfrac{\pi }{6} \right),\ \left( 2,\dfrac{\pi }{3} \right),\ \left( 3,\dfrac{\pi }{2} \right)$. The triangle $\Delta ABC$ formed by this coordinate can be seen in figure below:

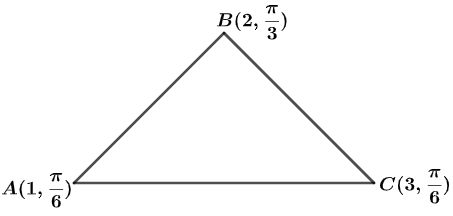
Now, first of all we will convert polar coordinates in to cartesian coordinates or X-Y coordinates using the formula of radian to degree conversion i.e. $\text{Degree, }{}^\circ = \dfrac{180}{\pi }\times \text{Radians}$
So, $\dfrac{180}{\pi }\times \dfrac{\pi }{6}={{30}^{\circ }}$, similarly, we can convert other radians into degree.
 Now, cartesian form of polar coordinates can be given as,
$\left( 1,\dfrac{\pi }{6} \right)=\left( 1\cos {{30}^{\circ }},1\sin {{30}^{\circ }} \right)$
$\Rightarrow \left( 1,\dfrac{\pi }{6} \right)=\left( \dfrac{\sqrt{3}}{2},\dfrac{1}{2} \right)$
$\left( 2,\dfrac{\pi }{3} \right)=\left( 2\cos {{60}^{\circ }},2\sin {{60}^{\circ }} \right)$
$\Rightarrow \left( 1,\dfrac{\pi }{6} \right)=\left( 1,\sqrt{3} \right)$
$\left( 3,\dfrac{\pi }{2} \right)=\left( 3\cos {{90}^{\circ }},3\sin {{90}^{\circ }} \right)$
$\Rightarrow \left( 1,\dfrac{\pi }{6} \right)=\left( 0,3 \right)$
Now, the vertices of the triangle in cartesian coordinate system can be given as, $\left( \dfrac{\sqrt{3}}{2},\dfrac{1}{2} \right),\left( 1,\sqrt{3} \right),\left( 0,3 \right)$. The tringle formed by this can be given as,

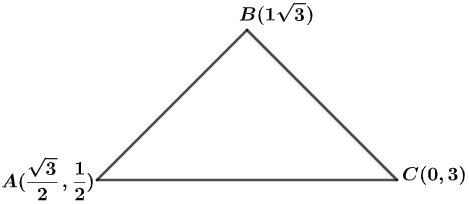
Now, the area of $\Delta ABC$ having vertices $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)$, can be given by determinant method of area of triangle i.e.
\[\text{Area of triangle, }\Delta =\dfrac{1}{2}\left| \begin{matrix}
   {{x}_{1}} & {{y}_{1}} & 1 \\
   {{x}_{2}} & {{y}_{2}} & 1 \\
   {{x}_{3}} & {{y}_{3}} & 1 \\
\end{matrix} \right|\] ……………………………….(i)
Simplifying the above equation, we get,
\[\Delta ABC=\dfrac{1}{2}\left( {{x}_{1}}\left| \begin{matrix}
   {{y}_{2}} & 1 \\
   {{y}_{3}} & 1 \\
\end{matrix} \right|-{{y}_{1}}\left| \begin{matrix}
   {{x}_{2}} & 1 \\
   {{x}_{3}} & 1 \\
\end{matrix} \right|-1\left| \begin{matrix}
   {{x}_{2}} & {{y}_{2}} \\
   {{x}_{3}} & {{y}_{3}} \\
\end{matrix} \right| \right)\] ……………………………(ii)
Where, ${{x}_{1}}=\dfrac{\sqrt{3}}{2},{{y}_{1}}=\dfrac{1}{2}$, ${{x}_{2}}=1,{{y}_{2}}=\sqrt{3}$, ${{x}_{3}}=0,{{y}_{3}}=3$
Substituting, the value of vertices derived as X-Y coordinates in expression (ii) and further equating, we get,
\[\Delta ABC=\dfrac{1}{2}\left( \dfrac{\sqrt{3}}{2}\left| \begin{matrix}
   \sqrt{3} & 1 \\
   3 & 1 \\
\end{matrix} \right|-\dfrac{1}{2}\left| \begin{matrix}
   1 & 1 \\
   0 & 1 \\
\end{matrix} \right|+1\left| \begin{matrix}
   1 & \sqrt{3} \\
   0 & 3 \\
\end{matrix} \right| \right)\]
\[=\dfrac{1}{2}\left| \left( \dfrac{\sqrt{3}}{2} \right)\left( \sqrt{3}-3 \right)-\dfrac{1}{2}\left( 1-0 \right)+1\left( 3-0 \right) \right|\]
\[=\dfrac{1}{2}\left| \dfrac{3}{2}-\dfrac{3\sqrt{3}}{2}-\dfrac{1}{2}+3 \right|\]
\[=\dfrac{1}{2}\left| 4-\dfrac{3\sqrt{3}}{2} \right|=\left( 2-\dfrac{3\sqrt{3}}{4} \right)\text{sq}\text{. units}\]
Hence, the area of triangle with polar coordinates $\left( 1,\dfrac{\pi }{6} \right),\ \left( 2,\dfrac{\pi }{3} \right),\ \left( 3,\dfrac{\pi }{2} \right)$ is \[\left( 2-\dfrac{3\sqrt{3}}{4} \right)\text{sq}\text{. units}\].

Note: Students must know the formula of area of triangle by determinant method. While using this method students must keep in mind that in the formula cartesian coordinates are understood, not polar coordinates. So, they should also know how to convert polar coordinates into cartesian coordinates, otherwise they might make mistakes and the answer will be wrong. So, students must keep all the things in mind to solve the problem easily.