Question

Find the area of triangle ABC where \[A\left( {1, - 4} \right)\], and mid-point of the sides through A being \[\left( {2, - 1} \right)\] and \[\left( {0, - 1} \right)\].

Answer 1

Hint: Here, we need to find the area of triangle ABC. We will use mid-point formula to find the vertices of the triangle. Then, we will use the formula for area of triangle using co-ordinates of the vertices of the triangle to find the required area of the triangle ABC

Formula Used:
 We will use the following formulas:
According to the mid-point formula, the co-ordinates of the mid-point of the line segment joining two points \[P\left( {{x_1},{y_1}} \right)\] and \[Q\left( {{x_2},{y_2}} \right)\] are given by \[\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)\].
The area of a triangle with having the vertices \[P\left( {{x_1},{y_1}} \right)\], \[Q\left( {{x_2},{y_2}} \right)\] and \[R\left( {{x_3},{y_3}} \right)\] is given by \[\dfrac{1}{2}\left| {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right|\].

Complete step-by-step answer:
Let the other vertex of the triangle be \[B\left( {a,b} \right)\] and \[C\left( {p,q} \right)\].
We can draw a triangle using the given information and then represent these points in the figure.

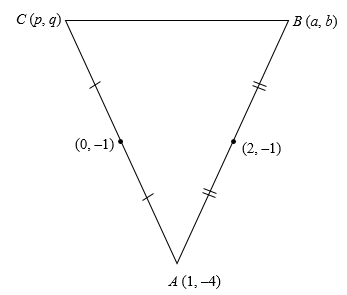
It is given that the mid-point of the sides through A being \[\left( {2, - 1} \right)\] and \[\left( {0, - 1} \right)\].
Thus, the mid-point of side AB is \[\left( {2, - 1} \right)\], and the mid-point of side AC is \[\left( {0, - 1} \right)\].
Now, we will use the mid-point formula in the line segment AB.
The co-ordinates of the mid-point of the line segment joining the points \[A\left( {1, - 4} \right)\] and \[B\left( {a,b} \right)\] are \[\left( {2, - 1} \right)\].
Therefore, substituting \[{x_1} = 1\], \[{y_1} = - 4\], \[{x_2} = a\], and \[{y_2} = b\] in the mid-point formula, \[\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)\], we get
\[ \Rightarrow \left( {2, - 1} \right) = \left( {\dfrac{{1 + a}}{2},\dfrac{{ - 4 + b}}{2}} \right)\]
Comparing the abscissa and the ordinate, we get the equations
\[ \Rightarrow 2 = \dfrac{{1 + a}}{2}\] and \[ - 1 = \dfrac{{ - 4 + b}}{2}\]
We will simplify these equations to get the co-ordinates of the vertex B of triangle ABC.
Multiplying both sides of the equation \[2 = \dfrac{{1 + a}}{2}\] by 2, we get
\[ \Rightarrow 4 = 1 + a\]
Subtracting 1 from both sides, we get
\[ \Rightarrow 4 - 1 = 1 + a - 1\]
Thus, we get
\[ \Rightarrow a = 3\]
Multiplying both sides of the equation \[ - 1 = \dfrac{{ - 4 + b}}{2}\] by 2, we get
\[ \Rightarrow - 2 = - 4 + b\]
Adding 4 on both sides, we get
\[ \Rightarrow - 2 + 4 = - 4 + b + 4\]
Thus, we get
\[ \Rightarrow b = 2\]
Substituting \[a = 3\] and \[b = 2\] in the point \[B\left( {a,b} \right)\], we get
\[\left( {a,b} \right) = \left( {3,2} \right)\]
Therefore, the co-ordinates of vertex B of the triangle ABC are \[\left( {3,2} \right)\].
Now, the co-ordinates of the mid-point of the line segment joining the points \[A\left( {1, - 4} \right)\] and \[C\left( {p,q} \right)\] are \[\left( {0, - 1} \right)\].
Therefore, substituting \[{x_1} = 1\], \[{y_1} = - 4\], \[{x_2} = p\], and \[{y_2} = q\] in the mid-point formula, we get
\[ \Rightarrow \left( {0, - 1} \right) = \left( {\dfrac{{1 + p}}{2},\dfrac{{ - 4 + q}}{2}} \right)\]
Comparing the abscissa and the ordinate, we get the equations
\[ \Rightarrow 0 = \dfrac{{1 + p}}{2}\] and \[ - 1 = \dfrac{{ - 4 + q}}{2}\]
We will simplify these equations to get the co-ordinates of the vertex B of triangle ABC.
Multiplying both sides of the equation \[0 = \dfrac{{1 + p}}{2}\] by 2, we get
\[ \Rightarrow 0 = 1 + p\]
Subtracting 1 from both sides of the equation, we get
\[ \Rightarrow 0 - 1 = 1 + p - 1\]
Thus, we get
\[ \Rightarrow p = - 1\]
Multiplying both sides of the equation \[ - 1 = \dfrac{{ - 4 + q}}{2}\] by 2, we get
\[ \Rightarrow - 2 = - 4 + q\]
Adding 4 on both sides of the equation, we get
\[ \Rightarrow - 2 + 4 = - 4 + q + 4\]
Thus, we get
\[ \Rightarrow q = 2\]
Substituting \[p = - 1\] and \[q = 2\] in the point \[C\left( {p,q} \right)\], we get
\[\left( {p,q} \right) = \left( { - 1,2} \right)\]
Therefore, the co-ordinates of vertex C of the triangle ABC are \[\left( { - 1,2} \right)\].
Thus, we get the three vertices of the triangle as \[A\left( {1, - 4} \right)\], \[B\left( {3,2} \right)\], and \[C\left( { - 1,2} \right)\].
Now, we will find the area of the triangle using the co-ordinates of the vertices.
Therefore, substituting \[{x_1} = 1\], \[{y_1} = - 4\], \[{x_2} = 3\], \[{y_2} = 2\], \[{x_3} = - 1\], and \[{y_3} = 2\] in the formula \[\dfrac{1}{2}\left| {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right|\], we get
\[ \Rightarrow \] Area of triangle ABC \[ = \dfrac{1}{2}\left| {1\left( {2 - 2} \right) + 3\left( {2 - \left( { - 4} \right)} \right) + \left( { - 1} \right)\left( { - 4 - 2} \right)} \right|\]
Simplifying the expressions in the parentheses, we get
\[ \Rightarrow \] Area of triangle ABC \[ = \dfrac{1}{2}\left| {1\left( {2 - 2} \right) + 3\left( {2 + 4} \right) + \left( { - 1} \right)\left( { - 4 - 2} \right)} \right|\]
Adding and subtracting the terms, we get
\[ \Rightarrow \] Area of triangle ABC \[ = \dfrac{1}{2}\left| {1\left( 0 \right) + 3\left( 6 \right) + \left( { - 1} \right)\left( { - 6} \right)} \right|\]
Multiplying the terms, we get
\[ \Rightarrow \] Area of triangle ABC \[ = \dfrac{1}{2}\left| {0 + 18 + 6} \right|\]
Adding the terms, we get
\[ \Rightarrow \] Area of triangle ABC \[ = \dfrac{1}{2}\left| {24} \right| = \dfrac{1}{2} \times 24\]
Therefore, we get
\[ \Rightarrow \] Area of triangle ABC \[ = 12\] square units
Thus, we get the area of triangle ABC as 12 square units.


Note: We used the terms ‘abscissa’ and ‘ordinate’ in the solution. The abscissa of a point \[\left( {x,y} \right)\] is \[x\], and the ordinate of a point \[\left( {x,y} \right)\] is \[y\].
The mid-point formula is derived from the section formula. According to the section formula, the co-ordinates of a point dividing the line segment joining two points \[P\left( {{x_1},{y_1}} \right)\] and \[Q\left( {{x_2},{y_2}} \right)\] in the ratio \[m:n\], are given by \[\left( {\dfrac{{m{x_1} + n{x_2}}}{{m + n}},\dfrac{{m{y_1} + n{y_2}}}{{m + n}}} \right)\]. If a point divides a line segment joining two points in the ratio 1: 1, then that point is the mid-point of the line segment.