Question

How do you find the area of the triangle given c= 4, A= 37 degrees, B= 69 degrees?

Answer 1

Hint: Here in this question, we have to find the area of the triangle using the formula of area of triangle i.e., \[Area = \dfrac{1}{2} \times base \times height\] , for finding the area we have to find the length using the trigonometric ratio. then substitute the given value of base and height on simplification using the basic multiplication operation we get the required area of the triangle.

Complete step by step solution:

The area of a triangle is defined as the total region that is enclosed by the three sides of any particular triangle. Basically, it is equal to half of the base times height, i.e., \[Area = \dfrac{1}{2} \times base \times height\] or \[A = \dfrac{1}{2} \times b \times h\] . Hence, to find the area of a tri-sided polygon, we have to know the base (b) and height (h) of it.
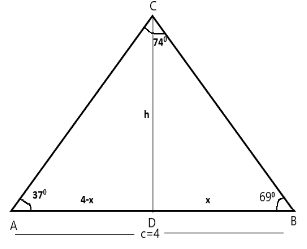
Consider triangle \[\Delta \,ABC\] where AB is the base of triangle i.e., \[c = 4\] then angle \[\left| \!{\underline {\,
  B \,}} \right. = {69^0}\] and \[\left| \!{\underline {\,
  A \,}} \right. = {37^0}\] now, find the angle between the \[\left| \!{\underline {\,
  C \,}} \right. \] .
As we know the Sum of internal angles in a triangle is \[{180^0}\] . i.e.,
 \[ \Rightarrow \,\,\left| \!{\underline {\,
  A \,}} \right. + \left| \!{\underline {\,
  B \,}} \right. + \left| \!{\underline {\,
  C \,}} \right. = {180^0}\]
 \[ \Rightarrow \,\,{37^0} + {69^0} + \left| \!{\underline {\,
  C \,}} \right. = {180^0}\]
 \[ \Rightarrow \,\,{106^0} + \left| \!{\underline {\,
  C \,}} \right. = {180^0}\]
 \[ \Rightarrow \,\,\left| \!{\underline {\,
  C \,}} \right. = {180^0} - {106^0}\]
 \[ \Rightarrow \,\,\left| \!{\underline {\,
  C \,}} \right. = {180^0} - {106^0}\]
 \[ \Rightarrow \,\,\left| \!{\underline {\,
  C \,}} \right. = {74^0}\]
And draw the line from point C to D which is perpendicular to the line AB i.e., height of the \[\Delta \,ABC\] is h
The distance between the DB is \[x\] and AD is \[4 - x\] .
Now consider the definition of trigonometric ratios tan.
 \[ \Rightarrow \,\tan = \dfrac{{opp}}{{adj}}\]
Consider the \[\Delta CDB\]
 \[ \Rightarrow \,\tan {69^0} = \dfrac{h}{x}\]
As by calculator \[\tan {69^0} = 2.60\] , then
 \[ \Rightarrow \,2.60 = \dfrac{h}{x}\]
 \[ \Rightarrow \,2.60 = \dfrac{h}{x}\]
 \[ \Rightarrow \,h = \,2.60x\] -----(1)
Again, consider the \[\Delta CAD\]
 \[ \Rightarrow \,\tan {37^0} = \dfrac{h}{{4 - x}}\]
As by calculator \[\tan {37^0} = 0.75\] , then
 \[ \Rightarrow \,0.75 = \dfrac{h}{{4 - x}}\]
 \[ \Rightarrow \,h = 0.75\left( {4 - x} \right)\]
 \[ \Rightarrow \,h = 3 - 0.75x\] ----(2)
From Equation (1) and (2), we can written as
 \[ \Rightarrow \,2.60x = 3 - 0.75x\]
Now find the \[x\] vale
 \[ \Rightarrow \,x = \dfrac{3}{{3.35}}\]
 \[ \Rightarrow \,x = 0.89\]
Substitute the \[x\] value in equation (1) to get the height of the \[\Delta \,ABC\] .
 \[ \Rightarrow \,h = \,2.60\left( {0.89} \right)\]
 \[ \Rightarrow \,h = \,2.314\]
Now find the area of \[\Delta \,ABC\] by using the formula of area of triangle is
 \[Area = \dfrac{1}{2} \times base \times height\]
The area of triangle \[\Delta \,ABC\] is
 \[ \Rightarrow \,\,Area = \dfrac{1}{2} \times AB \times CD\]
 \[ \Rightarrow \,\,Area = \dfrac{1}{2} \times 4 \times 2.314\]
 \[ \Rightarrow \,\,Area = 2 \times 2.314\]
On simplification, we get
 \[ \Rightarrow \,\,Area = 4.628\]
Hence, the area of the triangle is \[4.628\] Sq units.
So, the correct answer is “ \[4.628\] Sq units.”.

Note: While determining the area we use the formula. The formula is \[A = \dfrac{1}{2} \times b \times h\] . The unit for the perimeter will be the same as the unit of the length of a side or triangle. Whereas the unit for the area will be the square of the unit of the length of a triangle. We should not forget to write the unit.