Question

Find the area of the triangle \[ABC\] with \[A\left( {1, - 4} \right)\] and midpoints of sides through \[A\] being \[\left( {2, - 1} \right)\] and \[\left( {0, - 1} \right)\]

Answer 1

Hint:
Here, we are required to find the area of a triangle \[ABC\]. We will use the midpoint formula, and find the other two vertices of the given triangle. Then we will substitute the values in the formula of the area of the triangle and after solving it, we will get the required answer.

Formula Used:
We will use the following formulas:
1) Area of triangle \[ = \dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right]\]
2) Midpoint formula: Coordinates of midpoint \[D = \left( {\dfrac{{{A_1} + {A_2}}}{2},\dfrac{{{B_1} + {B_2}}}{2}} \right)\] where, \[\left( {{A_1},{B_1}} \right)\]and \[\left( {{A_2},{B_2}} \right)\] are the coordinates of the points \[A\]and \[B\] respectively.

Complete step by step solution:
We will draw a figure showing all the given points and conditions.

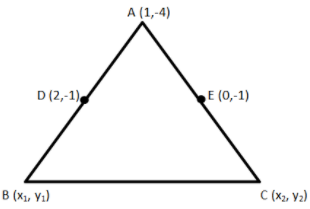
Now, since point \[D\left( {2, - 1} \right)\] is the midpoint of the side \[AB\].
Hence, substituting \[\left( {{A_1},{B_1}} \right) = \left( {1, - 4} \right)\] and \[\left( {{A_2},{B_2}} \right) = \left( {{x_1},{y_1}} \right)\] in the formula \[D = \left( {\dfrac{{{A_1} + {A_2}}}{2},\dfrac{{{B_1} + {B_2}}}{2}} \right)\], we get
Coordinates of point \[D = \left( {\dfrac{{1 + {x_1}}}{2},\dfrac{{ - 4 + {y_1}}}{2}} \right)\]
\[ \Rightarrow \left( {2, - 1} \right) = \left( {\dfrac{{1 + {x_1}}}{2},\dfrac{{ - 4 + {y_1}}}{2}} \right)\]
Now, comparing \[x\]and \[y\]coordinates, we get
\[ \Rightarrow 2 = \dfrac{{1 + {x_1}}}{2}\] and \[ - 1 = \dfrac{{ - 4 + {y_1}}}{2}\]
\[ \Rightarrow {x_1} = 3\] and \[{y_1} = 2\]
Hence, point \[B = \left( {3,2} \right)\].
Similarly, point \[E\left( {0, - 1} \right)\] is the midpoint of the side \[AC\].
Hence, by midpoint formula Coordinates of point \[E = \left( {\dfrac{{{A_1} + {A_2}}}{2},\dfrac{{{B_1} + {B_2}}}{2}} \right)\].
Hence, substituting \[\left( {{A_1},{B_1}} \right) = \left( {1, - 4} \right)\] and \[\left( {{A_2},{B_2}} \right) = \left( {{x_2},{y_2}} \right)\] in the above equation, we get,
Coordinates of point \[E = \left( {\dfrac{{1 + {x_2}}}{2},\dfrac{{ - 4 + {y_2}}}{2}} \right)\]
\[ \Rightarrow \left( {0, - 1} \right) = \left( {\dfrac{{1 + {x_2}}}{2},\dfrac{{ - 4 + {y_2}}}{2}} \right)\]
Now, comparing \[x\] and \[y\] coordinates,
\[ \Rightarrow 0 = \dfrac{{1 + {x_2}}}{2}\] and \[ - 1 = \dfrac{{ - 4 + {y_2}}}{2}\]
\[ \Rightarrow {x_2} = - 1\] and \[{y_2} = 2\]
Hence, point \[C = \left( { - 1,2} \right)\].
Now, substituting \[\left( {{x_1},{y_1}} \right) = \left( {1, - 4} \right)\], \[\left( {{x_2},{y_2}} \right) = \left( {3,2} \right)\] and \[\left( {{x_3},{y_3}} \right) = \left( { - 1,2} \right)\] in the formula area of triangle\[ = \dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right]\], we get,
Area of triangle \[ABC\]\[ = \dfrac{1}{2}\left[ {1\left( {2 - 2} \right) + 3\left( {2 + 4} \right) - 1\left( { - 4 - 2} \right)} \right]\]
Subtracting the terms in the bracket, we get
\[ \Rightarrow \] Area of triangle \[ABC\]\[ = \dfrac{1}{2}\left[ {3\left( 6 \right) - 1\left( { - 6} \right)} \right]\]
Multiplying the terms, we get
\[ \Rightarrow \] Area of triangle \[ABC\]\[ = \dfrac{1}{2}\left[ {18 + 6} \right]\]
Simplifying the expression, we get
\[ \Rightarrow \] Area of triangle \[ABC\]\[ = \dfrac{{24}}{2} = 12\]
Therefore, the area of the triangle \[ABC = 12\] square units.

Hence, the area of the triangle \[ABC\] with \[A\left( {1, - 4} \right)\] and midpoints of sides through \[A\] being \[\left( {2, - 1} \right)\] and \[\left( {0, - 1} \right)\] is 12 square units.

Note:
A triangle is a two dimensional geometric shape which has three sides. There are different types of triangle such as equilateral triangle, right-angled triangle, isosceles triangle etc. Here, we have not used the general formula of area of triangle i.e. \[A = \dfrac{1}{2} \times {\rm{base}} \times {\rm{height}}\] because the coordinate of the midpoint of sides is given. So, we have to find the coordinate of the vertices and then substitute these values area of triangle\[ = \dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right]\] to get the required area. We might make a mistake by using the coordinate of midpoint as the coordinate of vertices and substituting it in the formula. This will give use the wrong answer.