Question

Find the area of the trapezium-shaped field, the lengths of whose parallel sides are \[42\] meters and \[30\] meters and other sides are \[18\] meter and \[18\] meter.

Answer 1

Hint: Here we are asked to find the area of a field that is in the trapezium shape with the parallel side whose lengths are given. Since we don’t have any standard formula to find the area of the trapezium, we need to split the trapezium into a parallelogram and a triangle. Then using the formula of area of parallelogram and triangle we will find the area of a trapezium.
Formula Used: The formula that we need to know for this problem:
The area of a triangle: \[\sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} \]
\[a,b,c - \]sides of a triangle
\[s = \dfrac{{a + b + c}}{2}\]
The area of a parallelogram: \[b \times h\]
\[b - \]base
\[h - \]perpendicular height

Complete step-by-step solution:
It is given that the field is in the trapezium shape with the length of parallel sides \[42\] meter and \[30\] meter and the other parallel sides \[18\] meter and \[18\] meter.

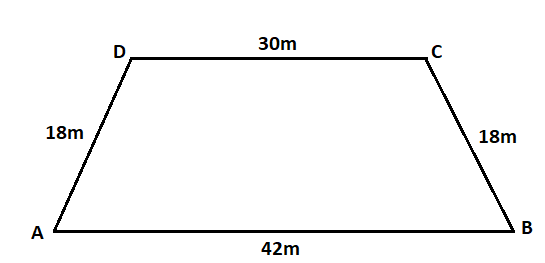
We aim to find the area of the field. Since we don’t have any standard formula to find the area of a trapezium, we need to split the trapezium into a parallelogram and a triangle.
Draw a line \[CE\parallel AD\] and a line \[CF \bot AB\].

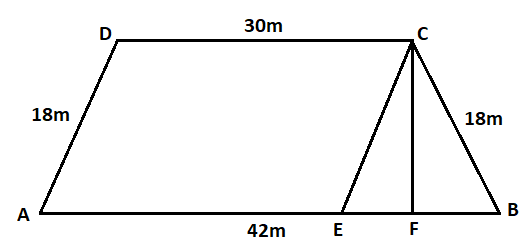
Now we have a parallelogram \[AECD\] and a triangle \[EBC\].
Now let’s find the areas of parallelogram and triangle.
Area of a triangle:
Sides of a triangle: \[BC = 18m\] \[CE\parallel AD \Rightarrow CE = 18m\] and \[EB = AB - AE = 42 - 30 = 12\] (Since \[AE\parallel DC \Rightarrow AE = 30m\])
Using the formula, the area of a triangle: \[\sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} = \sqrt {24\left( {24 - 18} \right)\left( {24 - 28} \right)\left( {24 - 12} \right)} \] where \[a,b,c - \]sides of a triangle and \[s = \dfrac{{a + b + c}}{2}\].
\[s = \dfrac{{18 + 18 + 12}}{2} = 24\]
Therefore, \[\sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} = \sqrt {24\left( {24 - 18} \right)\left( {24 - 18} \right)\left( {24 - 12} \right)} \]
On simplifying the above, we get
\[ \Rightarrow \sqrt {24\left( 6 \right)\left( 6 \right)\left( {12} \right)} \]
\[ \Rightarrow \sqrt {10368} \]
\[ \Rightarrow 101.82{m^2}\]
Thus, we have found the area of a \[\Delta EBC\].
Area of parallelogram:
The area of a parallelogram \[AECD = b \times h = AE \times CF\]
Since we don’t know the length of the perpendicular line \[CF\] let’s find it.
We know that another formula for a triangle is \[\dfrac{1}{2}bh\]. Since we know the area and the base of a triangle, we can find the height of the triangle.
\[\dfrac{1}{2}\left( {12} \right)h = 101.82\]
On simplifying the above, we get
\[h = 101.82 \times \dfrac{2}{{12}}\]
\[h = 16.9m\]
Now that we have the perpendicular height, let us find the area of a parallelogram.
\[b \times h = AE \times CF = 30 \times 16.9\]
On simplifying the above, we get
\[= 507{m^2}\]
Thus, we have the parallelogram \[AECD\].
Area of a trapezium: Area of parallelogram \[AECD\] \[ + \]area of a triangle \[\Delta EBC\]
\[= 507 + 101.82\]
\[= 610.92{m^2}\]
Hence, we have found the area of a field that is in trapezium shape.

Note: The parallel line and the perpendicular line has to be drawn on the correct side of the trapezium. An isosceles triangle is nothing but a triangle that has two equal sides. Also, we can find the area of an isosceles triangle using another formula \[\dfrac{b}{4}\sqrt {4{a^2} - {b^2}} \] where \[b - \]the base of a triangle, \[a - \]length of the same side.