Question

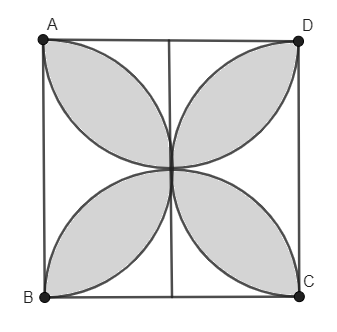
Find the area of the shaded region in the given figure, where ABCD is a square of side 14 cm, and semicircles are drawn with each side of the square as diameter.

Answer 1

Hint: Try to find the overlapping regions of the four semi-circles and figure out the relation of the shaded region with it.

Complete step by step answer:
Given:
ABCD is a square with each side measuring 14cm.
Semi-circles are drawn with each side of the square as diameter.
 So, the radius of each semi-circle = $\dfrac{\text{diameter}}{2}=\dfrac{14}{2}=7\text{ cm}$
Let’s start with the formula for the area of the square and the circle.
Area of a square with side ‘l’ $=l\times l$ .
Area of semi-circle with radius r = \[\dfrac{\pi {{r}^{2}}}{2}\] .
For our convenience, let us name the area of different regions in the figure.

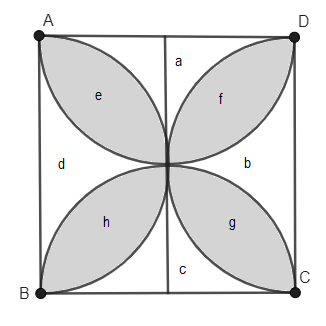
Area of square= $a+b+c+d+e+f+g+h$ .
Also, using the formula of area of a square;
Area of square ABCD= $l\times l=14\times 14=196\text{ c}{{\text{m}}^{2}}$ .
$\Rightarrow a+b+c+d+e+f+g+h=196\text{ c}{{\text{m}}^{2}}...............(i)$ .
Now, using the formula of area of semi-circle:
Area of semi-circles with BC as diameter $=h+b+f=\dfrac{\pi {{r}^{2}}}{2}=\dfrac{\pi \times {{7}^{2}}}{2}$ .
$\therefore h+b+f=\dfrac{49\pi }{2}\text{ c}{{\text{m}}^{2}}...............(ii)$
Area of semi-circles with CD as diameter $=e+a+f=\dfrac{\pi {{r}^{2}}}{2}=\dfrac{\pi \times {{7}^{2}}}{2}$ .
$\therefore e+a+f=\dfrac{49\pi }{2}\text{c}{{\text{m}}^{2}}................(iii)$
Area of semi-circles with AD as diameter $=e+d+g=\dfrac{\pi {{r}^{2}}}{2}=\dfrac{\pi \times {{7}^{2}}}{2}$.
$\therefore e+d+g=\dfrac{49\pi }{2}\text{c}{{\text{m}}^{2}}................(iv)$
Area of semi-circles with AB as diameter $=c+h+g=\dfrac{\pi {{r}^{2}}}{2}=\dfrac{\pi \times {{7}^{2}}}{2}$.
$\therefore c+h+g=\dfrac{49\pi }{2}\text{c}{{\text{m}}^{2}}................(v)$
Now, Adding equations (ii), (iii), (iv) and (v).
We get;
$a+b+c+d+2e+2f+2g+2h=\dfrac{4\times 49\pi }{2}$
 $\Rightarrow a+b+c+d+2e+2f+2g+2h=2\times 49\pi $
Substituting $\pi $ as $\dfrac{22}{7}$ , we get:
$a+b+c+d+2e+2f+2g+2h=2\times 49\times \dfrac{22}{7}$
$\Rightarrow a+b+c+d+2e+2f+2g+2h=308\text{ c}{{\text{m}}^{2}}...............(vi)$
Subtracting equation (i) from equation (iv):
\[a+b+c+d+2e+2f+2g+2h-(a+b+c+d+e+f+g+h)=308-196\]
\[\Rightarrow e+f+g+h=112\text{ c}{{\text{m}}^{2}}\]
And, $e+f+g+h$ is the area of the shaded region.

Therefore, we can conclude that the area of the shaded region is 112$c{{m}^{2}}$ .

Note: Choose the value of $\pi $ wisely, as it is a number that will decide whether your calculation gets complicated or simple to solve. Also, be sure to name the regions as this not only reduces your effort but also gives you a lot of clear idea of the figure.