Question

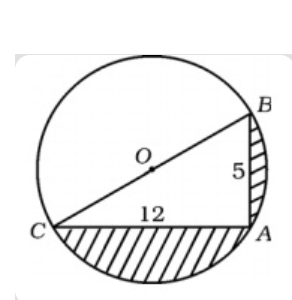
Find the area of the shaded region in the figure, if AB=5 cm, AC=12 cm and O is the centre of the circle.

Answer 1

Hint: In this question, we use the formula of the area of the semi circle and also the area of the right angle triangle. Area of semi circle is $\dfrac{{\pi {r^2}}}{2}$ and area of right angle triangle is $\dfrac{1}{2} \times \left( {{\text{Base}}} \right) \times \left( {{\text{Height}}} \right)$. In this question we also use the Pythagorean Theorem ${\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {{\text{Base}}} \right)^2}$.

Complete step-by-step answer:
Given, AB=5 cm, AC=12 cm and O is the centre of the circle.
To find the area of a semi circle we have to find the radius of the circle.
In $\vartriangle ABC$ we apply Pythagoras Theorem because angle subtended by a diameter on any point of circle is 900 and we know BC is a diameter of circle.
\[
  {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {{\text{Base}}} \right)^2} \\
   \Rightarrow {\left( {BC} \right)^2} = {\left( {AC} \right)^2} + {\left( {AB} \right)^2} \\
 \]
Use AB=5 cm, AC=12 cm
\[
   \Rightarrow {\left( {BC} \right)^2} = {\left( {12} \right)^2} + {\left( 5 \right)^2} \\
   \Rightarrow {\left( {BC} \right)^2} = 144 + 25 \\
   \Rightarrow {\left( {BC} \right)^2} = 169 \\
 \]
Take square root,
\[ \Rightarrow BC = 13cm\]
The Diameter of the circle is 13cm so the radius of the circle is 6.5cm.
Now, Area of semicircle $ = \dfrac{{\pi {r^2}}}{2}$
$ \Rightarrow \dfrac{{\pi \times {{\left( {6.5} \right)}^2}}}{2}$
Use value of $\pi = 3.14$
$
   \Rightarrow \dfrac{{3.14 \times {{\left( {6.5} \right)}^2}}}{2} \\
   \Rightarrow 66.3325c{m^2} \\
$
So, the area of the semicircle is 66.3325 $cm^2$.
Now we find area of right angle triangle $\vartriangle ABC$ ,
$
  {\text{Area of }}\vartriangle {\text{ABC}} = \dfrac{1}{2} \times \left( {{\text{Base}}} \right) \times \left( {{\text{Height}}} \right) \\
   \Rightarrow {\text{Area of }}\vartriangle {\text{ABC}} = \dfrac{1}{2} \times \left( {AC} \right) \times \left( {AB} \right) \\
   \Rightarrow {\text{Area of }}\vartriangle {\text{ABC}} = \dfrac{1}{2} \times \left( {12} \right) \times \left( 5 \right) \\
   \Rightarrow {\text{Area of }}\vartriangle {\text{ABC}} = 30c{m^2} \\
$
Now, the area of shaded region = Area of semi circle- area of right angle triangle $\vartriangle ABC$ .
\[
  {\text{Area of shaded region = }}66.3325 - 30 \\
   \Rightarrow {\text{Area of shaded region = 3}}6.3325c{m^2} \\
\]
So, the area of the shaded region is 36.3325 $cm^2$.

Note: Whenever we face such types of problems we use some important points. First we find the area of the semi circle and also find the area of the right angle triangle then subtract the area of the right angle triangle from the area of the semi circle. So, we will get the required answer.