Question

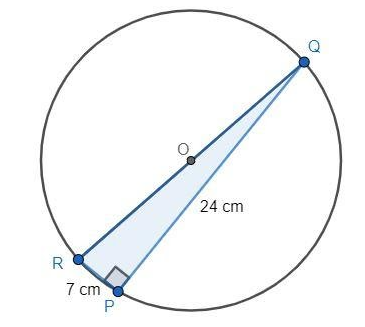
Find the area of the shaded region if \[PQ = 24{\rm{ cm}}\], \[PR = 7{\rm{ cm}}\] and \[O\] is the centre of the circle.

Answer 1

Hint:
First, we will find the area of semicircle on the right of diameter RQ. Then, we will find the area of triangle PQR and subtract it from the area of semicircle. We will obtain the area of the shaded region (area under chord PQ).
Formula used:
Pythagoras Theorem: In a right-angled triangle, \[{H^2} = {P^2} + {B^2}\] where \[H, P\] and \[B\] are the hypotenuse, perpendicular and base of the triangle respectively.
Area of a semicircle with radius \[r\] is \[\dfrac{{\pi {r^2}}}{2}\]
Area of a triangle is given by \[\dfrac{1}{2} \times b \times h\] where \[b\] and \[h\] are the base and height of the triangle respectively.

Complete step by step solution:

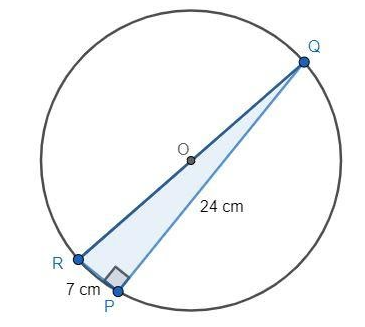
Any angle in a semicircle is always right. So, PR and PQ are perpendicular to each other. Thus, PQR is a right-angled triangle. Let us apply Pythagoras theorem on PQR. Substitute 24 for P and 7 for B in the first formula.
\[\begin{array}{l}{24^2} + {7^2} = R{Q^2} \\ \Rightarrow 576 + 49 = R{Q^2} \\ \Rightarrow 625 = R{Q^2} \\ \Rightarrow 25 = RQ\end{array}\]
We have found that the diameter of the circle RQ is 25 cm. The radius of the circle is half of its diameter. Let us find the radius of the circle:
\[\begin{array}{l}r = \dfrac{{25}}{2} \\ \Rightarrow r = 12.5\end{array}\]
The radius of the circle is \[12.5\] cm.
Let us find the area of the semi circle. We will substitute \[12.5\] for \[r\] in the second formula.
\[ \begin{array}{l}
{A_s} = \dfrac{{\pi {{\left( {12.5} \right)}^2}}}{2} \\
\Rightarrow {A_t} = \dfrac{1}{2} \times 7 \times 24 \\
\Rightarrow{A_t} = 84 \\
\Rightarrow {A_s} = 245.44\\
\end{array}\]
The area of the semi circle is \[245.44\] square centimetres.
Now, let us find the area of the triangle. Substitute 7 for \[b\] and 24 for \[h\] in the third formula.
 The area of the triangle is 84 square centimetres.
Let us find the area of shaded region by subtracting area of triangle from area of semi-circle:
\[\begin{array}{l} A = 245.44 - 84\\\Rightarrow A = 161.43\end{array}\]

\[\therefore \] Area of the shaded region is \[161.43{\rm{ c}}{{\rm{m}}^2}\].

Note:
We can make the mistake of using the formula for the area of a circle instead of the formula for the area of a semicircle. We need to be careful about this.