Question

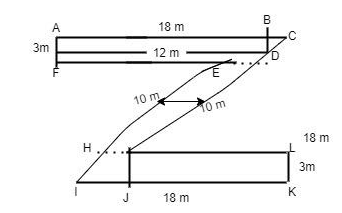
Find the area of the shaded region.

Answer 1

Hint: To find area of shaded region first calculate the individual area. $\text{Calculate Area of rectangles ABDF }\!\!\And\!\!\text{ HIJK}$(area of rectangle=$l\times b$)
   $\begin{align}
  & \text{also calculate area of triangle }HIJ\text{ }\!\!\And\!\!\text{ }BCD\text{ (area of triangle }=\frac{1}{2}\text{base}\times \text{altitude)} \\
 & \text{ }\!\!\And\!\!\text{ calculate area of parallelogram }EDGH\text{(area of triangle=}\frac{1}{2}\times Base\times Altitude) \\
\end{align}$

Formula used:
\[\text{Area of rectangle }=Base\times Altitude\]
$\text{Area of triangle}=\frac{1}{2}\times Base\times Altitude$
$\text{Area of parallelogram}=Base\times Altitude$

Complete step-by-step answer:
 $\text{Area of rectangle }ABDF=AB\times AF$
Where
$AB+FD=12\text{ }m\text{ }\!\!\And\!\!\text{ AF=3 }m$
$\therefore \text{Area of rectangle }ABDF=12\times 3$
$=36\text{ }{{m}^{2}}$ ……. (1)
Similarly
$\text{Area of rectangle }HLKJ=JK\times LK$
$JK=HL=FD=12\text{ }m\text{ }=12\times 3=36\text{ }{{m}^{2}}$ …… (2)
$\text{ }\!\!\And\!\!\text{ }LK=3\text{ }m$
$\text{Also Area of }\vartriangle +BCD=\frac{1}{2}\times BD\times BC$
               $=\frac{1}{2}\times 3\times 6=9\text{ }{{m}^{2}}.....(3)$
$\begin{align}
  & BD=3\text{ }m \\
 & BC=AC-AB \\
 & \text{ }=18-12 \\
 & \text{ }=6\text{ }m \\
\end{align}$
$\begin{align}
  & \text{Area of }\vartriangle HIJ=\frac{1}{2}\times HJ\times JI \\
 & =\frac{1}{2}\times 3\times 6 \\
 & =9{{m}^{2}}.......(4) \\
\end{align}$
$\begin{align}
  & LK=HJ=3\text{ }m \\
 & JI=KI-KJ \\
 & \text{ }=18-12 \\
 & \text{ }=6\text{ }m \\
\end{align}$

$\begin{align}
  & \text{Area of parallelogram }HGDE=Base\times Altitude \\
 & =GD\times \bot \text{ distance}\left( \text{perpendicular distance 3 }m\text{ given} \right) \\
 & =10\times 3 \\
 & =30{{m}^{2}}...........(5) \\
\end{align}$
$\text{Total area of shaded region}=\text{Area }ABDF+\text{Area }HLKJ+\text{Area }\vartriangle BCD+\text{Area }\vartriangle HIJ+\text{Area }HGDE$$=36+36+9+9+30$
$=120\text{ }{{m}^{2}}$

Note: Always solve this question by breaking the pictures in small pictures whose areas are known and add or subtract accordingly. In this question we calculate the area of rectangle ABDF, area of rectangle HLKJ, area of triangle BCD, area of triangle HIJ and area of the parallelogram HGDE and then we add all these areas to find the area of shaded regions in the figure above.