Question

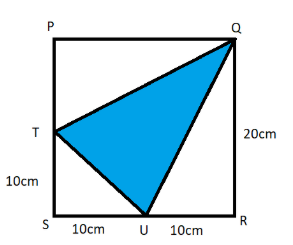
Find the area of the shaded portion in the following figure :

Answer 1

Hint: First, understand that PQRS is a square of side length 20 cm. Find its area using the formula: Area of a square = ${{\left( side \right)}^{2}}$. Then find the area of the triangles QRU, TSU, and QPT using the formula: area of a triangle = $\dfrac{1}{2}\times $ base $\times $ height. Then use the formula:
Area of shaded region = Area of square PQRS - (Area of triangle QRU + Area of triangle TSU + Area of triangle QPT) to find the final answer.

Complete step-by-step answer:

In this question, we are given a figure.
We need to find the area of the shaded portion in the figure.
From the figure, we can see the following:
SR = 10 + 10 = 20 cm
QR = 20 cm
TS = 10 cm
So, PT = 10 cm
PQ = 20 cm
As we can see that PQRS is a square
We already know that the area of a square is equal to the square of its sides.
i.e. Area of a square = ${{\left( side \right)}^{2}}$
In the given question, PQRS is a square with side length = 20 cm.
So, area of the square PQRS = 20 $\times $ 20 = 400 sq. cm.
 We know that area of a triangle is half of the product of its base and its height.
i.e. area of a triangle = $\dfrac{1}{2}\times $ base $\times $ height.
Using this formula, we will find the following:
Area of triangle QRU = $\dfrac{1}{2}\times $ 10 $\times $ 20 = 100 sq. cm.
Area of triangle TSU = $\dfrac{1}{2}\times $ 10 $\times $ 10 = 50 sq. cm.
Area of triangle QPT = $\dfrac{1}{2}\times $ 10 $\times $ 20 = 100 sq. cm.
Now,
Area of shaded region = Area of square PQRS - (Area of triangle QRU + Area of triangle TSU + Area of triangle QPT ) = 400 − (100 + 50 + 100) = 400 – 250 = 150 sq. cm.
So, the area of the shaded portion = 150 sq. cm.

Note: In this question, it is very important to understand and know the areas of which figures to add or subtract from an existing expression. Keep in mind that whenever you are taking the area of a region, does it have overlap with other regions or not and how to counter this. In this way, you can keep track of all the regions and hence, can avoid making mistakes.