
Find the area of the segment AYB, shown in figure, if radius of the circle is 12 cm and \[\angle AOB={{120}^{\circ }}\]. Use \[\pi =\dfrac{22}{7}\].

Answer
613.8k+ views
Hint: First of all we will find the area of sector AOB and then we subtract the area of triangle AOB to get the required area of segment AYB. The area of sector subtending an angle ‘\[\theta \]’ and radius ‘r’ is given as:
Area \[=\pi {{r}^{2}}\times \left( \dfrac{{{\theta }^{\circ }}}{{{360}^{\circ }}} \right)\]
Also, we know that the area of a triangle having sides a, b and \[\theta \] as the angle between them is equal to \[\left( \dfrac{1}{2}ab\times \sin \theta \right)\].
Complete step-by-step answer:
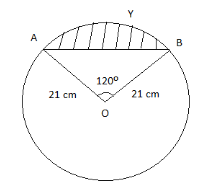
We have been asked to find the area of segment AYB from the figure given with radius of circle as 21 cm and \[\angle AOB={{120}^{\circ }}\].
First of all we will find the area of sector using the formula \[\pi {{r}^{2}}\times \left( \dfrac{{{\theta }^{\circ }}}{{{360}^{\circ }}} \right)\] where r is the radius of the circle and \[\theta \] is the angle subtended by the arc corresponding to the sector.
Area of sector AOB \[=\pi \times {{\left( 21 \right)}^{2}}\times \dfrac{{{120}^{\circ }}}{{{360}^{\circ }}}\]
Since we have \[\pi =\dfrac{22}{7}\]
\[\Rightarrow \dfrac{22}{7}\times 21\times 21\times \dfrac{1}{3}=462c{{m}^{2}}\]
Now we know the area of a triangle having sides a, b and angle between them as \[\theta \] is given by \[\left( \dfrac{1}{2}ab\times \sin \theta \right)\].
\[\Rightarrow \] Area of \[\Delta ABC\]\[=\dfrac{1}{2}\times 21\times 21\times \sin {{120}^{\circ }}\]
Since \[\sin {{120}^{\circ }}=\dfrac{\sqrt{3}}{2}\] and \[\sqrt{3}=1.732\]
\[\Rightarrow \dfrac{1}{2}\times 21\times 21\times \dfrac{\sqrt{3}}{2}=\dfrac{441\times 1.732}{4}=190.95c{{m}^{2}}\] (approx.)
For the figure we can say that the area of segment AYB is equal to the difference of area of sector AOB and area of \[\Delta ABC\].
\[\Rightarrow \]Area of segment AYB \[=\left( 462-190.95 \right)c{{m}^{2}}=271.05c{{m}^{2}}\]
Therefore, the area of the segment is equal to \[271.05c{{m}^{2}}\] approximately.
Note: Be careful while doing calculation and substitute the value of pi \[\left( \pi \right)\] is equal to \[\dfrac{22}{7}\] which is given to us. Don’t use the value of pi \[\left( \pi \right)\] as 3.14 instead of \[\dfrac{22}{7}\]. Also, remember that, the area of a triangle when we have been given 2 sides a, b and the angle between them as ‘\[\theta \]’ is given by \[\dfrac{1}{2}\times \left( ab \right)\times \sin \theta \].
Area \[=\pi {{r}^{2}}\times \left( \dfrac{{{\theta }^{\circ }}}{{{360}^{\circ }}} \right)\]
Also, we know that the area of a triangle having sides a, b and \[\theta \] as the angle between them is equal to \[\left( \dfrac{1}{2}ab\times \sin \theta \right)\].
Complete step-by-step answer:
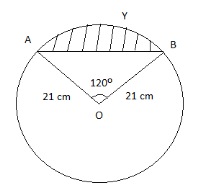
We have been asked to find the area of segment AYB from the figure given with radius of circle as 21 cm and \[\angle AOB={{120}^{\circ }}\].

First of all we will find the area of sector using the formula \[\pi {{r}^{2}}\times \left( \dfrac{{{\theta }^{\circ }}}{{{360}^{\circ }}} \right)\] where r is the radius of the circle and \[\theta \] is the angle subtended by the arc corresponding to the sector.
Area of sector AOB \[=\pi \times {{\left( 21 \right)}^{2}}\times \dfrac{{{120}^{\circ }}}{{{360}^{\circ }}}\]
Since we have \[\pi =\dfrac{22}{7}\]
\[\Rightarrow \dfrac{22}{7}\times 21\times 21\times \dfrac{1}{3}=462c{{m}^{2}}\]
Now we know the area of a triangle having sides a, b and angle between them as \[\theta \] is given by \[\left( \dfrac{1}{2}ab\times \sin \theta \right)\].
\[\Rightarrow \] Area of \[\Delta ABC\]\[=\dfrac{1}{2}\times 21\times 21\times \sin {{120}^{\circ }}\]
Since \[\sin {{120}^{\circ }}=\dfrac{\sqrt{3}}{2}\] and \[\sqrt{3}=1.732\]
\[\Rightarrow \dfrac{1}{2}\times 21\times 21\times \dfrac{\sqrt{3}}{2}=\dfrac{441\times 1.732}{4}=190.95c{{m}^{2}}\] (approx.)
For the figure we can say that the area of segment AYB is equal to the difference of area of sector AOB and area of \[\Delta ABC\].
\[\Rightarrow \]Area of segment AYB \[=\left( 462-190.95 \right)c{{m}^{2}}=271.05c{{m}^{2}}\]
Therefore, the area of the segment is equal to \[271.05c{{m}^{2}}\] approximately.
Note: Be careful while doing calculation and substitute the value of pi \[\left( \pi \right)\] is equal to \[\dfrac{22}{7}\] which is given to us. Don’t use the value of pi \[\left( \pi \right)\] as 3.14 instead of \[\dfrac{22}{7}\]. Also, remember that, the area of a triangle when we have been given 2 sides a, b and the angle between them as ‘\[\theta \]’ is given by \[\dfrac{1}{2}\times \left( ab \right)\times \sin \theta \].
Recently Updated Pages
Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Trending doubts
State and explain Ohms law class 10 physics CBSE

Distinguish between soap and detergent class 10 chemistry CBSE

a Why did Mendel choose pea plants for his experiments class 10 biology CBSE

What is a "free hit" awarded for in limited-overs cricket?

Draw the diagram of the sectional view of the human class 10 biology CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE




