Answer
Verified448.2k+ views
Hint:
Here we will use the formula for the area of a sector of a circle. We will substitute the values of \[\theta \] and \[r\] in the formula. We will simplify the equation and calculate the area.
Formulas used:
We will use the following formulas:
The diameter of a circle is 2 times its radius:
\[d = 2r\]
Area of a sector of a circle with radius \[r\] and angle \[\theta \] is given by \[A = \pi {r^2}\dfrac{\theta }{{360}}\].
Complete step by step solution:
First we will draw the circle showing the sector.
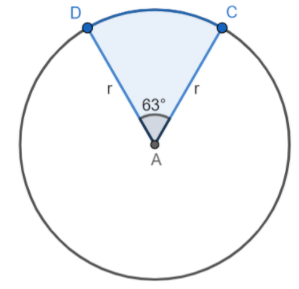
We will find the radius of the circle.
Substituting 20 for diameter in \[d = 2r\], we get
\[\begin{array}{l}20 = 2r\\ \Rightarrow 10 = r\end{array}\]
The radius of the circle is 10 cm.
We will now find the area of the given sector.
By substituting \[63^\circ \] for \[\theta \], 10 for \[r\] and \[\dfrac{{22}}{7}\] for \[\pi \] in the formula \[A = \pi {r^2}\dfrac{\theta }{{360}}\], we get
\[ \Rightarrow A = \dfrac{{22}}{7} \times {\left( {10} \right)^2} \times \dfrac{{63}}{{360}}\]
Simplifying the expression, we get
\[\begin{array}{l} \Rightarrow A = \dfrac{{22 \times 100}}{{40}}\\ \Rightarrow A = 55{\rm{ c}}{{\rm{m}}^2}\end{array}\]
$\therefore $ Option C is the correct option.
Note:
If we are unable to recall the formula for the area of a sector, we can derive it using the unitary method.
We know that the area of a circle is \[\pi {r^2}\] where \[r\] is its radius. We also know that the angle of a full circle is \[360^\circ \]. We can say that a circle is a sector with an angle of 360 degrees.
The area of a sector with an angle of 360 degrees is \[\pi {r^2}\].
The area of a sector with an angle of 1 degree will be \[\dfrac{1}{{360^\circ }} \cdot \pi {r^2}\].
The area of a sector with an angle of \[\theta \] degrees will be:
\[\begin{array}{l} \Rightarrow A = \theta \times \dfrac{{\pi {r^2}}}{{360}}\\ \Rightarrow A = \dfrac{\theta }{{360}} \times \pi {r^2}\end{array}\]
Here we will use the formula for the area of a sector of a circle. We will substitute the values of \[\theta \] and \[r\] in the formula. We will simplify the equation and calculate the area.
Formulas used:
We will use the following formulas:
The diameter of a circle is 2 times its radius:
\[d = 2r\]
Area of a sector of a circle with radius \[r\] and angle \[\theta \] is given by \[A = \pi {r^2}\dfrac{\theta }{{360}}\].
Complete step by step solution:
First we will draw the circle showing the sector.
We will find the radius of the circle.
Substituting 20 for diameter in \[d = 2r\], we get
\[\begin{array}{l}20 = 2r\\ \Rightarrow 10 = r\end{array}\]
The radius of the circle is 10 cm.
We will now find the area of the given sector.
By substituting \[63^\circ \] for \[\theta \], 10 for \[r\] and \[\dfrac{{22}}{7}\] for \[\pi \] in the formula \[A = \pi {r^2}\dfrac{\theta }{{360}}\], we get
\[ \Rightarrow A = \dfrac{{22}}{7} \times {\left( {10} \right)^2} \times \dfrac{{63}}{{360}}\]
Simplifying the expression, we get
\[\begin{array}{l} \Rightarrow A = \dfrac{{22 \times 100}}{{40}}\\ \Rightarrow A = 55{\rm{ c}}{{\rm{m}}^2}\end{array}\]
$\therefore $ Option C is the correct option.
Note:
If we are unable to recall the formula for the area of a sector, we can derive it using the unitary method.
We know that the area of a circle is \[\pi {r^2}\] where \[r\] is its radius. We also know that the angle of a full circle is \[360^\circ \]. We can say that a circle is a sector with an angle of 360 degrees.
The area of a sector with an angle of 360 degrees is \[\pi {r^2}\].
The area of a sector with an angle of 1 degree will be \[\dfrac{1}{{360^\circ }} \cdot \pi {r^2}\].
The area of a sector with an angle of \[\theta \] degrees will be:
\[\begin{array}{l} \Rightarrow A = \theta \times \dfrac{{\pi {r^2}}}{{360}}\\ \Rightarrow A = \dfrac{\theta }{{360}} \times \pi {r^2}\end{array}\]