Question

Find the area of the rhombus whose perimeter is equal to $48$ units, and the sum of the lengths of the diagonals is equal to $26$?

Answer 1

Hint: The diagonals of a rhombus bisects each other in two equal parts and at right angles to each other. The two diagonals of a Rhombus divide it into four right angled triangles. In a right angled triangle, Pythagoras theorem is that the sum of squares of two sides is equal to square hypotenuse. We use these logics and apply basic formulas to find the required values.

Formula used:
Area of a Rhombus with diagonals $d_1$ and $d_2$ is $=d_1 \times d_2 \dfrac{1}{2}$
Pythagoras theorem gives $\text{Hypotenuse}^2=\text{Perpendicular}^2+\text{Base}^2$
We will use the identity \[{(a + b)^2} = {a^2} + {b^2} + 2ab\] .

Complete step by step answer:
We have given the perimeter of the Rhombus $=48$ units.
Since all sides of the rhombus are equal, each side of the rhombus \[ = \dfrac{{\text{Perimeter}}}{4}\]
Each side of the rhombus $=12$
We know that diagonals of the Rhombus bisect each other at right angles.
Let’s assume the diagonals as $d_1$ and $d_2$.
The below diagram shows the required Rhombus

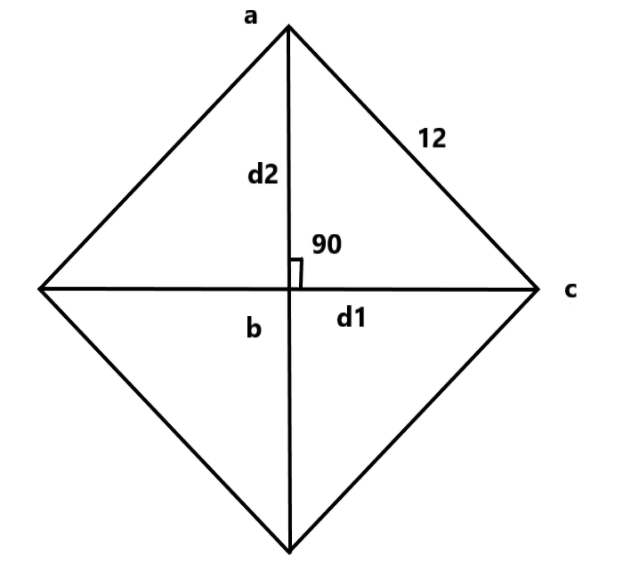
We have given, the sum of diagonals is $26$.
So, $d_1 ^2 + d_2 ^2 =26$
Now, as triangle $abc$ is right angled triangle,
From Pythagoras theorem, $\text{Hypotenuse}^2=\text{Perpendicular}^2+\text{Base}^2$
$d_1 ^2 + d_2 ^2= 12^2$
\[ \Rightarrow d_1 ^2 + d_2 ^2= 144 \times 4\]
\[ \Rightarrow d_1 ^2 + d_2 ^2 = 576\]
We know that area of rhombus in terms of diagonals is given by
\[ = \dfrac{1}{2} \times d_1 \times d_2\]
Now, we have to find the value of the product of $d_1$ and $d_2$.
we know the identity
\[{(a + b)^2} = {a^2} + {b^2} + 2ab\]
We rearrange them
$ \Rightarrow {(a + b)^2} - {a^2} - {b^2} = 2ab$
We have divided both sides by 4,
$ \Rightarrow \dfrac{1}{4}\left\{ {{{(a + b)}^2} - {a^2} - {b^2}} \right\} = \dfrac{1}{2}ab$
Using the above formula, we substitute \[a = d_1\] and \[b = d_2\] .
\[ \Rightarrow \dfrac{1}{2} \times {d_{{1}}} \times {d_{{2}}} = \dfrac{1}{4}\left\{ {{{({d_{{1}}} + {d_{{2}}})}^2} - ({d_{{1}}}^2 + {d_{{2}}}^2)} \right\}\]
We have substituted \[{d_{{1}}} + {d_{{2}}} = 26\] and \[{d_{{1}}}^2 + {d_{{2}}}^2 = 576\]
\[ = \dfrac{1}{4}\left\{ {{{(26)}^2} - 576} \right\}\]
\[ = \dfrac{1}{4}\left\{ {676 - 576} \right\}\]
\[ = 25sq.units\]
Therefore, the Area of the Rhombus is $25 \, sq.units$.

Note:
Area of Rhombus can also be obtained by product of base and height. In a rhombus all sides are equal, so the base is the same as its side. The altitude (height) of a rhombus is the perpendicular distance from the base to the opposite side. Every Square is a Rhombus but every Rhombus is not a Square.