Find the area of the region $\left\{ \left( x,y \right):{{x}^{2}}+{{y}^{2}}\le 4,x+y\ge 2 \right\}$.
Answer
Verified508.8k+ views
Hint: We solve this question starting with finding the point of intersection of the given curves. Then we draw the graph for the function and plot the required region. Then from the graph we find the limits of the region and we integrate the function and find the area as required. While integrating we use the formula $\int{\sqrt{{{a}^{2}}-{{x}^{2}}}dx=\dfrac{x}{2}}\sqrt{{{a}^{2}}-{{x}^{2}}}-\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{a}+c$.
Complete step by step answer:
We need to find the area of region given by $\left\{ \left( x,y \right):{{x}^{2}}+{{y}^{2}}\le 4,x+y\ge 2 \right\}$.
As we see at the given region, it consists of two curves ${{x}^{2}}+{{y}^{2}}\le 4$ and $x+y\ge 2$.
The first curve ${{x}^{2}}+{{y}^{2}}\le 4$ consists of all the points inside the circle ${{x}^{2}}+{{y}^{2}}=4$.
The second curve $x+y\ge 2$ consists of all the points that lie above the line $x+y=2$.
So, we need to consider the region that is common to both the regions from the given two curves.
Let us consider the point of intersection of the two curves ${{x}^{2}}+{{y}^{2}}=4$ and $x+y=2$.
$\begin{align}
& \Rightarrow x+y=2\Leftrightarrow y=2-x \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}=4 \\
& \Rightarrow {{x}^{2}}+{{\left( 2-x \right)}^{2}}=4 \\
& \Rightarrow {{x}^{2}}+{{x}^{2}}-4x+4=4 \\
& \Rightarrow 2{{x}^{2}}-4x=0 \\
& \Rightarrow 2x\left( x-2 \right)=0 \\
& \Rightarrow x\left( x-2 \right)=0 \\
& \Rightarrow x=0,2 \\
\end{align}$
Now substitute the values of x in y, then we get
When x=0, $y=2-x=2-0=2$
When $x=2$, we get $y=2-x=2-2=0$
So, the points of intersection of the two curves are $\left( 0,2 \right)$ and $\left( 2,0 \right)$.
Now, let us look at the graph of the given regions and the curves.
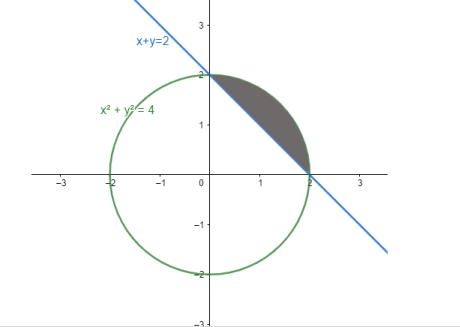
As we see in the graph, to obtain the area of our required region, we need to subtract the area of region bounded by the line an x-axis between x=0 and x=2 from the area of region bounded by circle and x-axis between x=0 and x=2 and above the x-axis.
So, First let us calculate the area of the region bounded by the circle and x-axis between x=0 and x=2 and above the x-axis.
Area of region bounded by any function $f\left( x \right)$ and x-axis between x=a and x=b can be given as $\int\limits_{a}^{b}{f\left( x \right)dx}$
Using the above formula, it can be calculated as
$\int\limits_{0}^{2}{\sqrt{4-{{x}^{2}}}dx}$
Now let us consider the formula
$\int{\sqrt{{{a}^{2}}-{{x}^{2}}}dx=\dfrac{x}{2}}\sqrt{{{a}^{2}}-{{x}^{2}}}-\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{a}+c$
Here let a=2.
Then
$\begin{align}
& \Rightarrow \int{\sqrt{{{2}^{2}}-{{x}^{2}}}dx=\dfrac{x}{2}}\sqrt{{{2}^{2}}-{{x}^{2}}}-\dfrac{{{2}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{2}+c \\
& \Rightarrow \int{\sqrt{4-{{x}^{2}}}dx=\dfrac{x}{2}}\sqrt{4-{{x}^{2}}}-\dfrac{4}{2}{{\sin }^{-1}}\dfrac{x}{2}+c \\
& \Rightarrow \int{\sqrt{4-{{x}^{2}}}dx=\dfrac{x}{2}}\sqrt{4-{{x}^{2}}}-2{{\sin }^{-1}}\dfrac{x}{2}+c \\
\end{align}$
Using this we can find the value of $\int\limits_{0}^{2}{\sqrt{4-{{x}^{2}}}dx}$
$\begin{align}
& \Rightarrow \int\limits_{0}^{2}{\sqrt{4-{{x}^{2}}}dx}=\left[ \dfrac{x}{2}\sqrt{4-{{x}^{2}}}-2{{\sin }^{-1}}\dfrac{x}{2}+c \right]_{0}^{2} \\
& \Rightarrow \int\limits_{0}^{2}{\sqrt{4-{{x}^{2}}}dx}=\left[ \dfrac{2}{2}\sqrt{4-{{2}^{2}}}-2{{\sin }^{-1}}\dfrac{2}{2}+c \right]-\left[ \dfrac{0}{2}\sqrt{4-{{0}^{2}}}-2{{\sin }^{-1}}\dfrac{0}{2}+c \right] \\
& \Rightarrow \int\limits_{0}^{2}{\sqrt{4-{{x}^{2}}}dx}=\left[ \sqrt{4-4}-2{{\sin }^{-1}}1+c \right]-\left[ 0-2{{\sin }^{-1}}0+c \right] \\
& \Rightarrow \int\limits_{0}^{2}{\sqrt{4-{{x}^{2}}}dx}=2{{\sin }^{-1}}0-2{{\sin }^{-1}}1 \\
& \Rightarrow \int\limits_{0}^{2}{\sqrt{4-{{x}^{2}}}dx}=0-2\left( \dfrac{\pi }{2} \right) \\
& \Rightarrow \int\limits_{0}^{2}{\sqrt{4-{{x}^{2}}}dx}=-\pi \\
\end{align}$
As the area is a positive quantity, we take the modulus of obtained value. So, the area of the region by circle is $\pi $ square units.
Now let us consider the area of the region bounded by the line an x-axis between x=0 and x=2.
Using the formula for the area of region bounded by any function $f\left( x \right)$ and x-axis between x=a and x=b can be given as $\int\limits_{a}^{b}{f\left( x \right)dx}$.
So, we can find the area by integrating it as $\int\limits_{0}^{2}{\left( 2-x \right)dx}$.
So, calculating it we get
\[\begin{align}
& \Rightarrow \int\limits_{0}^{2}{\left( 2-x \right)dx} \\
& \Rightarrow \int\limits_{0}^{2}{2dx}-\int\limits_{0}^{2}{xdx} \\
& \Rightarrow \left[ 2x \right]_{0}^{2}-\left[ \dfrac{{{x}^{2}}}{2} \right]_{0}^{2} \\
& \Rightarrow \left[ 4-0 \right]-\left[ \dfrac{4}{2}-\dfrac{0}{2} \right] \\
& \Rightarrow 4-2 \\
& \Rightarrow 2 \\
\end{align}\]
So, the area obtained from the line is 2 square units.
Now, subtracting the area of region bounded by the line an x-axis between x=0 and x=2 from the area of region bounded by circle and x-axis between x=0 and x=2 and above the x-axis.
\[\Rightarrow \pi -2\]
So, Area of the required region is \[\pi -2\] square units.
So, the correct answer is \[\pi -2\] square units.
Note: There is also a shortcut method for calculating the area of the required region. As we look at the graph of the curves, we can see that our required area can be written as,
(Area of quarter circle) – (Area of triangle formed by the line, x-axis and y-axis)
We can calculate the area of the circle using the formula $\text{Area of circle}=\pi \times {{\left( \text{radius} \right)}^{2}}$. Here the radius of the circle is 2 units. Then the area of the circle is $4\pi $ square units. Then the area of the quarter circle is $\pi $ square units.
We can also find the area of triangle by using the formula $\text{Area of triangle}=\dfrac{1}{2}\times \left( \text{base} \right)\times \left( \text{height} \right)$.
Here from the graph we can say that the base and height of the triangle are 2 units.
Then the area of triangle is
$\begin{align}
& \Rightarrow \dfrac{1}{2}\times 2\times 2 \\
& \Rightarrow 2 \\
\end{align}$
So, by subtracting the two areas we get the area of our required region, which is \[\pi -2\] square units.
Hence, the answer is \[\pi -2\] square units.
Complete step by step answer:
We need to find the area of region given by $\left\{ \left( x,y \right):{{x}^{2}}+{{y}^{2}}\le 4,x+y\ge 2 \right\}$.
As we see at the given region, it consists of two curves ${{x}^{2}}+{{y}^{2}}\le 4$ and $x+y\ge 2$.
The first curve ${{x}^{2}}+{{y}^{2}}\le 4$ consists of all the points inside the circle ${{x}^{2}}+{{y}^{2}}=4$.
The second curve $x+y\ge 2$ consists of all the points that lie above the line $x+y=2$.
So, we need to consider the region that is common to both the regions from the given two curves.
Let us consider the point of intersection of the two curves ${{x}^{2}}+{{y}^{2}}=4$ and $x+y=2$.
$\begin{align}
& \Rightarrow x+y=2\Leftrightarrow y=2-x \\
& \Rightarrow {{x}^{2}}+{{y}^{2}}=4 \\
& \Rightarrow {{x}^{2}}+{{\left( 2-x \right)}^{2}}=4 \\
& \Rightarrow {{x}^{2}}+{{x}^{2}}-4x+4=4 \\
& \Rightarrow 2{{x}^{2}}-4x=0 \\
& \Rightarrow 2x\left( x-2 \right)=0 \\
& \Rightarrow x\left( x-2 \right)=0 \\
& \Rightarrow x=0,2 \\
\end{align}$
Now substitute the values of x in y, then we get
When x=0, $y=2-x=2-0=2$
When $x=2$, we get $y=2-x=2-2=0$
So, the points of intersection of the two curves are $\left( 0,2 \right)$ and $\left( 2,0 \right)$.
Now, let us look at the graph of the given regions and the curves.
As we see in the graph, to obtain the area of our required region, we need to subtract the area of region bounded by the line an x-axis between x=0 and x=2 from the area of region bounded by circle and x-axis between x=0 and x=2 and above the x-axis.
So, First let us calculate the area of the region bounded by the circle and x-axis between x=0 and x=2 and above the x-axis.
Area of region bounded by any function $f\left( x \right)$ and x-axis between x=a and x=b can be given as $\int\limits_{a}^{b}{f\left( x \right)dx}$
Using the above formula, it can be calculated as
$\int\limits_{0}^{2}{\sqrt{4-{{x}^{2}}}dx}$
Now let us consider the formula
$\int{\sqrt{{{a}^{2}}-{{x}^{2}}}dx=\dfrac{x}{2}}\sqrt{{{a}^{2}}-{{x}^{2}}}-\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{a}+c$
Here let a=2.
Then
$\begin{align}
& \Rightarrow \int{\sqrt{{{2}^{2}}-{{x}^{2}}}dx=\dfrac{x}{2}}\sqrt{{{2}^{2}}-{{x}^{2}}}-\dfrac{{{2}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{2}+c \\
& \Rightarrow \int{\sqrt{4-{{x}^{2}}}dx=\dfrac{x}{2}}\sqrt{4-{{x}^{2}}}-\dfrac{4}{2}{{\sin }^{-1}}\dfrac{x}{2}+c \\
& \Rightarrow \int{\sqrt{4-{{x}^{2}}}dx=\dfrac{x}{2}}\sqrt{4-{{x}^{2}}}-2{{\sin }^{-1}}\dfrac{x}{2}+c \\
\end{align}$
Using this we can find the value of $\int\limits_{0}^{2}{\sqrt{4-{{x}^{2}}}dx}$
$\begin{align}
& \Rightarrow \int\limits_{0}^{2}{\sqrt{4-{{x}^{2}}}dx}=\left[ \dfrac{x}{2}\sqrt{4-{{x}^{2}}}-2{{\sin }^{-1}}\dfrac{x}{2}+c \right]_{0}^{2} \\
& \Rightarrow \int\limits_{0}^{2}{\sqrt{4-{{x}^{2}}}dx}=\left[ \dfrac{2}{2}\sqrt{4-{{2}^{2}}}-2{{\sin }^{-1}}\dfrac{2}{2}+c \right]-\left[ \dfrac{0}{2}\sqrt{4-{{0}^{2}}}-2{{\sin }^{-1}}\dfrac{0}{2}+c \right] \\
& \Rightarrow \int\limits_{0}^{2}{\sqrt{4-{{x}^{2}}}dx}=\left[ \sqrt{4-4}-2{{\sin }^{-1}}1+c \right]-\left[ 0-2{{\sin }^{-1}}0+c \right] \\
& \Rightarrow \int\limits_{0}^{2}{\sqrt{4-{{x}^{2}}}dx}=2{{\sin }^{-1}}0-2{{\sin }^{-1}}1 \\
& \Rightarrow \int\limits_{0}^{2}{\sqrt{4-{{x}^{2}}}dx}=0-2\left( \dfrac{\pi }{2} \right) \\
& \Rightarrow \int\limits_{0}^{2}{\sqrt{4-{{x}^{2}}}dx}=-\pi \\
\end{align}$
As the area is a positive quantity, we take the modulus of obtained value. So, the area of the region by circle is $\pi $ square units.
Now let us consider the area of the region bounded by the line an x-axis between x=0 and x=2.
Using the formula for the area of region bounded by any function $f\left( x \right)$ and x-axis between x=a and x=b can be given as $\int\limits_{a}^{b}{f\left( x \right)dx}$.
So, we can find the area by integrating it as $\int\limits_{0}^{2}{\left( 2-x \right)dx}$.
So, calculating it we get
\[\begin{align}
& \Rightarrow \int\limits_{0}^{2}{\left( 2-x \right)dx} \\
& \Rightarrow \int\limits_{0}^{2}{2dx}-\int\limits_{0}^{2}{xdx} \\
& \Rightarrow \left[ 2x \right]_{0}^{2}-\left[ \dfrac{{{x}^{2}}}{2} \right]_{0}^{2} \\
& \Rightarrow \left[ 4-0 \right]-\left[ \dfrac{4}{2}-\dfrac{0}{2} \right] \\
& \Rightarrow 4-2 \\
& \Rightarrow 2 \\
\end{align}\]
So, the area obtained from the line is 2 square units.
Now, subtracting the area of region bounded by the line an x-axis between x=0 and x=2 from the area of region bounded by circle and x-axis between x=0 and x=2 and above the x-axis.
\[\Rightarrow \pi -2\]
So, Area of the required region is \[\pi -2\] square units.
So, the correct answer is \[\pi -2\] square units.
Note: There is also a shortcut method for calculating the area of the required region. As we look at the graph of the curves, we can see that our required area can be written as,
(Area of quarter circle) – (Area of triangle formed by the line, x-axis and y-axis)
We can calculate the area of the circle using the formula $\text{Area of circle}=\pi \times {{\left( \text{radius} \right)}^{2}}$. Here the radius of the circle is 2 units. Then the area of the circle is $4\pi $ square units. Then the area of the quarter circle is $\pi $ square units.
We can also find the area of triangle by using the formula $\text{Area of triangle}=\dfrac{1}{2}\times \left( \text{base} \right)\times \left( \text{height} \right)$.
Here from the graph we can say that the base and height of the triangle are 2 units.
Then the area of triangle is
$\begin{align}
& \Rightarrow \dfrac{1}{2}\times 2\times 2 \\
& \Rightarrow 2 \\
\end{align}$
So, by subtracting the two areas we get the area of our required region, which is \[\pi -2\] square units.
Hence, the answer is \[\pi -2\] square units.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success
Master Class 11 Accountancy: Engaging Questions & Answers for Success
Master Class 11 Social Science: Engaging Questions & Answers for Success
Master Class 11 Economics: Engaging Questions & Answers for Success
Master Class 11 Physics: Engaging Questions & Answers for Success
Master Class 11 Biology: Engaging Questions & Answers for Success
Trending doubts
Father of Indian ecology is a Prof R Misra b GS Puri class 12 biology CBSE
Who is considered as the Father of Ecology in India class 12 biology CBSE
Enzymes with heme as prosthetic group are a Catalase class 12 biology CBSE
A deep narrow valley with steep sides formed as a result class 12 biology CBSE
An example of ex situ conservation is a Sacred grove class 12 biology CBSE
Why is insulin not administered orally to a diabetic class 12 biology CBSE