Question

Find the area of the quadrilateral whose diagonal is of length 70 m and length of the perpendiculars drawn from the opposite vertices on the diagonal are of lengths 42 m and 50 m respectively.

Answer 1

Hint: A diagonal divides a quadrilateral into two triangles, both separated by the common side to both the triangles.Calculate the area of both the triangles using the formula $\dfrac{1}{2} \times b \times h$ and add them to get the area of the quadrilateral.

Complete step-by-step solution:
Let ABCD be the quadrilateral where BD is the diagonal and AE and CF are the perpendiculars drawn from the opposite vertices on the diagonal.

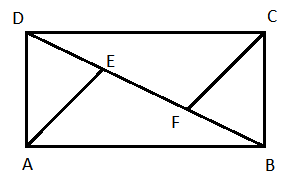
For \[\vartriangle ABD\], base $BD = 70$m and height $AE = 50$$ m $
Area of \[\vartriangle ABD\]$ = \dfrac{1}{2} \times 70 \times 50 = 1750$$ m^2 $
For \[\vartriangle BCD\], base $BD = 70$m and height $CF = 42$$ m $
Area of \[\vartriangle BCD\]$ = \dfrac{1}{2} \times 70 \times 42 = 1470$$ m^2 $
Area of quadrilateral $ABCD = $ Area of \[\vartriangle ABD\]$ + $ Area of \[\vartriangle BCD\]$ = 1750 + 1470 = 3220$$ m^2 $

Note:There is another approach to calculate the area of a quadrilateral.
Area of a quadrilateral is also given by $\dfrac{1}{2} \times $Diagonal $ \times $Sum of perpendiculars on the diagonal
Area of quadrilateral $ABCD = $$\dfrac{1}{2} \times 70 \times \left( {50 + 42} \right) = 35 \times 92 = 3220$$ m^2 $