Question

Find the area of the quadrilateral field ABCD whose sides $ AB = 40\;m,\;{\text{BC = 28 m, CD = 15 m, AD = 9 m}} $ and $ \angle A = 90^\circ $

Answer 1

Hint: First of all draw a diagram with the help of the given dimensions and find out the correlation to find out the area of the quadrilateral. Also, here quadrilateral is divided in two parts of triangle and area of triangle is found by half into altitude and base and second by Heron’s area formula.

Complete step-by-step answer:

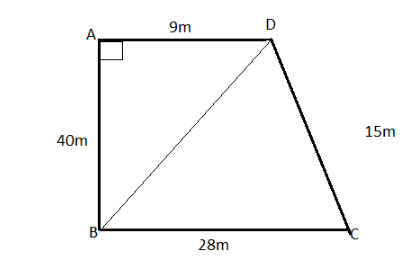
As shown in the above figure, in $ \Delta BAD,\;\angle {\text{A = 90}}^\circ $ and AD is base and AB is the altitude.
Therefore, Area of $ \Delta BAD = \dfrac{1}{2} \times AD \times AB $
Place given values in the above equation-
Area of $ \Delta BAD = \dfrac{1}{2} \times 9 \times 40 $
Find the factors in the numerator part on the right hand side of the equation.
Area of $ \Delta BAD = \dfrac{1}{2} \times 9 \times 20 \times 2 $
Common factors from the numerator and the denominator cancel each other. Therefore remove from the numerator and the denominator.
 $ \therefore $ Area of $ \Delta BAD = 9 \times 20 $
 $ \therefore $ Area of $ \Delta BAD = 180\;{m^2} $ ..... (A)
Now, using Pythagoras theorem in $ \Delta BAD $ ,
 $ B{D^2} = A{B^2} + A{D^2} $
Place the values in the above equation –
  $ B{D^2} = {40^2} + {9^2} $
Simplify the equation –
 $
  B{D^2} = 1600 + 81 \\
  B{D^2} = 1681 \;
  $
Take square-root on both the sides of the equation-
 $
  \sqrt {B{D^2}} = \sqrt {1681} \\
  \sqrt {B{D^2}} = \sqrt {{{41}^2}} \;
  $
Square and square-root cancel each other.
 $ \Rightarrow BD = 41m $
Also, In $ \Delta BDC, $ Semi-perimeter of the triangle is the sum of all the three sides divided by two.
 $ s = \dfrac{1}{2}(BD + DC + BC) $
Place values in the above equation -
 $ s = \dfrac{1}{2}(41 + 28 + 15) $
Simplify the above equation
 $
  s = \dfrac{1}{2}(84) \\
  s = 42\;{\text{m}} \;
  $
By using the Heron’s formula –
Area of $ \Delta BDC, $
 $ A = \sqrt {s(s - b)(s - c)(s - d)} $
Where “b” is the measure of side CD
“c” is the measure of side BD
“d” is the measure of side BC
Place values in the above equation –
 $ A = \sqrt {42(42 - 15)(42 - 28)(42 - 41)} $
Simplify the above equation –
\[
  A = \sqrt {42(27)(14)(1)} \\
  A = \sqrt {15876} \\
  A = \sqrt {{{126}^2}} \;
 \]
 Square and square-root cancel each other on the right hand side of the equation –
 $ A = 126\;{m^2}\;{\text{ }}.....{\text{ (B)}} $
Area of $ \square ABCD $ $ = Area{\text{ of }}\Delta BAD{\text{ + }}Area{\text{ of }}\Delta BCD $
By using the equation (A) and (B)
Area of $ \square ABCD = 180 + 126 $
Area of $ \square ABCD = 306\;{m^2} $
So, the correct answer is “ $ 306\;{m^2} $ ”.

Note: Know the concepts of square and square-root and apply accordingly. You can find the square-root by finding the factors of the numbers and making the pair of two. Also, do not forget to write an appropriate unit after the solution.