Question

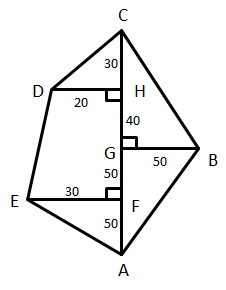
Find the area of the pentagonal field shown alongside in figure. Dimensions are in meters.

A) \[7000{{\rm{m}}^2}\]
B) \[7550{{\rm{m}}^2}\]
C) \[5650{{\rm{m}}^2}\]
D) \[6500{{\rm{m}}^2}\]

Answer 1

Hint:
Here, we are required to find the area of the given pentagonal field which is divided into triangles and trapezium whose dimensions are given in meters. We will use the formula of area of right angled triangles and the area of trapezium. Substituting the dimensions in the formulas will give us the required areas of different triangles and the trapezium. We will add all the obtained areas together to find the required area of the pentagonal field which consists of these areas.

Formula Used:
We will use the following formulas:
1) Area of a right angled triangle \[ = \dfrac{1}{2} \times b \times h\], where \[b\] is the base and \[h\] is the height of the triangle.
2) Area of trapezium \[ = \dfrac{1}{2} \times s \times h\], where \[s\] is the sum of parallel sides of the trapezium and \[h\] is the height of trapezium.

Complete Step by Step Solution:
For finding the area of the given pentagonal field, we will add the areas of the three triangles mentioned below and then, we will add the area of the trapezium.
Hence, area of triangle \[ABC = \dfrac{1}{2} \times b \times h\]…………………..\[\left( 1 \right)\]
Where, base, \[b = AC\] and height, \[h = BG\]
According to the figure,
\[AC = AF + FG + GH + HC\]
Now substituting \[AF = 50\], \[FG = 50\], \[GH = 40\] and \[HC = 30\] in the above equation, we get
\[ \Rightarrow AC = 50 + 50 + 40 + 30\]
Adding the terms, we get
\[ \Rightarrow AC = 170\]
Also, the height, \[BG = 50\]
Substituting \[AC = 170\] and \[BG = 50\] in the equation \[\left( 1 \right)\], we get
\[ \Rightarrow \] The area of the triangle \[ABC\] \[ = \dfrac{1}{2} \times 170 \times 50\]
Multiplying the terms, we get
 \[ \Rightarrow \] The area of the triangle \[ABC\] \[ = 4250{{\rm{m}}^2}\]………………………… \[\left( 2 \right)\]
Now, similarly, area of triangle \[AFE = \dfrac{1}{2} \times AF \times FE\]
\[ \Rightarrow \] The area of triangle \[AFE\] \[ = \dfrac{1}{2} \times 50 \times 30\]
\[ \Rightarrow \] The area of triangle \[AFE\] \[ = 750{{\rm{m}}^2}\]……………………………..\[\left( 3 \right)\]
Now, area of triangle \[CHD\] \[ = \dfrac{1}{2} \times CH \times HD\]
\[ \Rightarrow \] The area of triangle \[CHD\]\[ = \dfrac{1}{2} \times 30 \times 20\]
\[ \Rightarrow \] The area of triangle \[CHD\] \[ = 300{{\rm{m}}^2}\]…………………………..\[\left( 4 \right)\]
Now we will find the area of trapezium.
We know that the area of trapezium \[ = \dfrac{1}{2} \times s \times h\]
Hence, area of trapezium \[EFHD\] \[ = \dfrac{1}{2} \times \left( {HD + FE} \right) \times FH\]
\[ \Rightarrow \] Area of trapezium \[EFHD\] \[ = \dfrac{1}{2} \times \left( {20 + 30} \right) \times \left( {FG + GH} \right)\]
Substituting and adding the terms, we get
\[ \Rightarrow \] Area of trapezium \[EFHD\]\[ = \dfrac{1}{2} \times \left( {50} \right) \times \left( {50 + 40} \right)\]
Again adding the terms, we get
\[ \Rightarrow \] Area of trapezium \[EFHD\] \[ = \dfrac{1}{2} \times 50 \times 90\]
Multiplying the terms, we get
\[ \Rightarrow \] Area of trapezium \[EFHD\] \[ = 2250{{\rm{m}}^2}\]……………………………\[\left( 5 \right)\]
From the figure we can see that the area of pentangonal field is equal to sum of all areas of triangles and trapezuim. Therefore
The area of the pentagonal field $=ar\left( \vartriangle ABC \right)+ar\left( \vartriangle AFE \right)+ar\left( \vartriangle CHD \right)+ar\left( \text{trapezium}EFHD \right)$
Substituting the values of area from equation \[\left( 2 \right)\], \[\left( 3 \right)\], \[\left( 4 \right)\] and \[\left( 5 \right)\] in the above equation, we get, we get
Area of the pentagonal field \[ = \left( {4250 + 750 + 300 + 2250} \right)\]
Adding all the terms, we get
\[ \Rightarrow \] Area of the pentagonal field \[ = 7550{{\rm{m}}^2}\]
Hence, the required area of the given pentagonal field is \[7550{{\rm{m}}^2}\].

Therefore, option B is the correct answer.

Note:
In geometry, pentagon is a five sided shape. It has its own formula of calculating its area but when it is divided into further shapes such as triangles, squares, trapeziums, etc. then finding its area becomes quite easy. This is because of the fact that we have been using the formulas of the area of triangles or trapeziums quite regularly and they are easy to learn and hence, finding such areas and adding them is not considered to be a huge task. But, we should keep in mind that the lengths should be substituted in the formulas carefully because if for example the height is 40 but we have taken it as 30 then, this could change our area completely and hence, making our answer wrong.