Question

Find the area of the given figure.

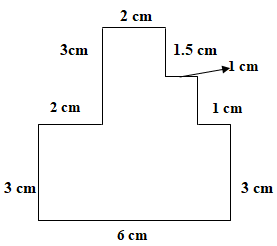
A. \[25.5{\rm{c}}{{\rm{m}}^2}\]
B. \[23.5{\rm{c}}{{\rm{m}}^2}\]
C. \[25{\rm{c}}{{\rm{m}}^2}\]
D. \[24{\rm{c}}{{\rm{m}}^2}\]

Answer 1

Hint: Here we will first divide the given figure into three rectangles and name them. Then we will use the formula for the area of the rectangle in all the three rectangles to find respective areas. Finally, we will add all the areas to get the required answer.

Complete step-by-step answer:
We will first name the end point of the figures and also divide the figure in three parts as follows:

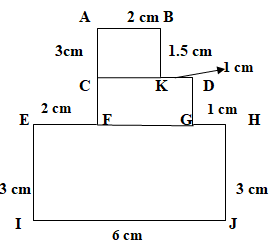
Now we will calculate the area of the figure in three parts.
First, we will calculate the area of rectangle ABCD.
Now,
Area of rectangle ABDC \[ = l \times b = AB \times AC\]
Substituting \[AB = 2\] and \[AC = 1.5\] in the above formula, we get
\[ \Rightarrow \] Area of rectangle ABCD \[ = 2 \times 1.5\]
Multiplying the terms, we get
\[ \Rightarrow \] Area of rectangle ABCD \[ = 3{\rm{c}}{{\rm{m}}^2}\]……………...\[\left( 1 \right)\]
Now, we will calculate the area of the rectangle CDFG.
We will first find the length of \[DG\] and \[FG\].
\[DG = AF - BK\]
Substituting the values, we get
\[ \Rightarrow DG = 3 - 1.5 = 1.5{\rm{cm}}\]
\[FG = IJ - \left( {EF + GH} \right)\]
Substituting the values, we get
\[ \Rightarrow FG = 6 - \left( {2 + 1} \right) = 3{\rm{cm}}\]
Area of rectangle CDGF \[ = l \times b = DG \times FG\]
Substituting \[DG = 1.5\] and \[FG = 3\] in the above formula, we get
\[ \Rightarrow \] Area of rectangle CDFG \[ = 1.5 \times 3\]
Multiplying the terms, we get
\[ \Rightarrow \] Area of rectangle CDFG \[ = 4.5{\rm{c}}{{\rm{m}}^2}\] ……….…..\[\left( 2 \right)\]
Now, we will calculate the area of the rectangle EHJI.
Area of rectangle EHJI \[ = l \times b = EH \times EI\]
Substituting \[EH = 6\] and \[EI = 3\] in the above formula, we get
\[ \Rightarrow \] Area of rectangle EHJI \[ = 6 \times 3\]
Multiplying the terms, we get
\[ \Rightarrow \] Area of rectangle EHJI \[ = 18{\rm{c}}{{\rm{m}}^2}\]…………..\[\left( 3 \right)\]
Finally, we will add all the areas of all the parts from the equation \[\left( 1 \right)\], \[\left( 2 \right)\] and \[\left( 3 \right)\] to get the total area of the figure.
Area of the figure \[ = \left( {4.5 + 3 + 18} \right){\rm{c}}{{\rm{m}}^2}\]

Adding the terms, we get
\[ \Rightarrow \] Area of the figure \[ = 25.5{\rm{c}}{{\rm{m}}^2}\]

Note:
When the figure given to is not in a shape whose area we know in that case we divide the figure as per our requirement to solve it easily. We could have divided the figure vertically to form four rectangles also but we choose the easy way where we have to find the area of only three rectangles. A rectangle is a quadrilateral having four sides with four right angles. It is a special case of a parallelogram which has a pair of adjacent sides at a perpendicular angle.